![]() The Proca-formulation of electrodynamics allows to account for a hypothetical massive photon. This formulation lead to astonishing experiments but is formally equivalent to the London theory of superconductivity. Learn in this problem how a magnetic field is expelled from a superconductor by "massive photons".
The Proca-formulation of electrodynamics allows to account for a hypothetical massive photon. This formulation lead to astonishing experiments but is formally equivalent to the London theory of superconductivity. Learn in this problem how a magnetic field is expelled from a superconductor by "massive photons".
Problem Statement
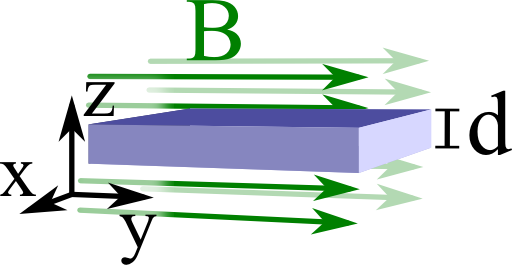 A superconducting half-plane is terminated at z = 0. Outside of the superconductor, there is a magnetostatic field
A superconducting half-plane is terminated at z = 0. Outside of the superconductor, there is a magnetostatic field
\[\mathbf{B}\left(\mathbf{r}\right)=B_{0}\mathbf{e}_{y}\]
parallel to the surface. Inside the superconductor, the Proca equation
\[\left(\Delta-\mu_{\mathrm{L}}^{2}\right)\mathbf{A}\left(\mathbf{r}\right) = 0\]
shall be applicable.
Calculate the magnetic induction with respect to the London penetration depth \(\lambda_{\mathrm{L}}=1/\mu_{\mathrm{L}}\).
Now consider the case if the superconductor is a slab with a finite thickness d, centered at z = 0. What does the induction look like now? Calculate an effective current j(r) inside the superconductor consistent with the calculated magnetic induction.
Discuss qualitatively how the magnetic field and current should look like if one replaces the superconducting slab with a superconducting wire of some radius.
Background: Photon Mass and Superconductivity
If photons had a nonvanishing mass, the electromagnetic fields would show different characteristics than those we are used to: a wavelength dependence of the speed of light, modifications of Coulomb's and Ampères law and thus different fields for charges and dipoles and so on. Without a doubt, the question for a photon mass is very fundamental. Here, however, we can use it to explain superconductivity following the Londons. For much more information please have a look at The "Mass" of the Photon - Magnetic Fields in Superconductors.
Hints
Outside of the superconductor we only have the field at hand. In our formulation, the Proca equation was given in terms of the vector potential. Given this expression,
\[\left(\Delta-\mu_{\mathrm{L}}^{2}\right)\mathbf{A}\left(\mathbf{r}\right)=0\]
which equation holds for the magnetic induction?
Solution
Inside the superconducter, the Proca equation
\[\left(\Delta-\mu_{\mathrm{L}}^{2}\right)\mathbf{A}\left(\mathbf{r}\right) = 0\]
holds for the vector potential A(r) with the London penetration depth \(\lambda_{\mathrm{L}}=1/\mu_{\mathrm{L}}\).
Now, we might take the curl of it and find that it also holds for the magnetic induction,
\[\begin{eqnarray*}0&=&\nabla\times\left(\Delta-\mu_{\mathrm{L}}^{2}\right)\mathbf{A}\left(\mathbf{r}\right)\\&=&\left(\Delta-\mu_{\mathrm{L}}^{2}\right)\nabla\times\mathbf{A}\left( \mathbf{r}\right) \\ & = &\left(\Delta-\mu_{\mathrm{L}}^{2}\right)\mathbf{B}\left(\mathbf{r}\right)\ .\end{eqnarray*}\]
Here, we have made use of Schwarz's theorem which allows us to interchange partial derivatives. It also becomes evident that without external currents,
\[\mathbf{j}_{\mathrm{ext}}\left(\mathbf{r}\right)=0\]
the effect of the superconducting material is included in \(\mu_{\mathrm{L}}\) - the tangential part of the magnetic induction has to be continuous.
The Superconducting Half-Space
This is the main information we have to use for the first part of the problem. So, if an external magnetic field
\[\mathbf{B}_{0}\left(\mathbf{r}\right)=B_{0}\mathbf{e}_{y}\]
is present, we have to match it to the physical solution of the equation we just derived. Because of the translation symmetry of the problem, the variation can only be in z direction, hence we know that the latter equation reduces to
\[\left(\partial_{zz}-\mu_{\mathrm{L}}^{2}\right)B_{y}\left(z\right) = 0\ \mathrm{for}\ z\leq0\ .\]
Using the ansatz \(B_{y}\left(z\right)=B_{y}^{0}\exp\left(\kappa z\right)\), we find
\[B_{y}\left(z\right) = B_{1}e^{\mu_{\mathrm{L}}z}+B_{2}e^{-\mu_{\mathrm{L}}z}\ \mathrm{for}\ z\leq0\ .\]
Requiring finiteness of the magnetic field for \(z\rightarrow-\infty\), we can drop the second term.
At z=0, the magnitude is given by \(B_{0}\) and hence we find the required
\[\mathbf{B}\left(\mathbf{r}\right) = B_{0}\mathbf{e}_{y}\begin{cases}1 & z>0\\e^{-\mu_{\mathrm{L}}\left|z\right|} & z\leq0\end{cases}\ .\]
So the field inside the superconductor falls off exponentially.
We remind ourselves that \(\mu_{\mathrm{L}}=1/\lambda_{\mathrm{L}}\) and can see directly that the London penetration depth is really some kind of penetration distance of the magnetic field into the superconductor.
Slab and Wire Geometries
Now that we know the easiest possible example we can advance to the case of a thin superconducting slab. Then again, inside the superconductor the equation
\[\left(\partial_{zz}-\mu_{\mathrm{L}}^{2}\right)B_{y}\left(z\right) = 0\ \mathrm{for}\ \left|z\right|\leq d/2\]
holds and we find the solutions to be again of the form
\[B_{y}\left(z\right) = B_{1}e^{\mu_{\mathrm{L}}z}+B_{2}e^{-\mu_{\mathrm{L}}z}\ \mathrm{for}\ \left|z\right|\leq d/2\ .\]
Since at \(z=\pm d/2\) and \(B_{y}=B_{0}\), \(B_{1}=B_{2}=B_{0}\) we conclude
\[\begin{eqnarray*}B_{y}\left(z\right)&=&B_{0}\frac{e^{\mu_{\mathrm{L}}z}+e^{-\mu_{\mathrm{L}}z}}{e^{\mu_{\mathrm{L}}d/2}+e^{-\mu_{\mathrm{L}}d/2}}\\&=&B_{0}\frac{\cosh\mu_{\mathrm{L}}z}{\cosh\mu_{L}d/2}\ \mathrm{for}\ \left|z\right|\leq d/2\end{eqnarray*}\]
using an appropriate normalization. Finally,
\[\mathbf{B}\left(\mathbf{r}\right) = B_{0}\mathbf{e}_{y}\begin{cases}1 & \left|z\right|>d/2\\\frac{\cosh\mu_{\mathrm{L}}z}{\cosh\mu_{L}d/2} & \left|z\right|\leq d/2\end{cases}\ .\]
In the model of a superconductor we have employed so far, we have no explicit expression for the current.
However, since we found the magnetic induction we might assign this field a conductive current using Ampère's law
 \[\begin{eqnarray*}\nabla\times\mathbf{B}\left(\mathbf{r}\right)&=&\mu_{0}\mathbf{j}_{\mathrm{cond}}\left(\mathbf{r}\right)\ ,\ \mathrm{so}\\\mathbf{j}_{\mathrm{cond}}\left(\mathbf{r}\right) & = &\frac{B_{0}}{\mu_{0}}\nabla\times\left(\frac{\cosh\mu_{\mathrm{L}}z}{\cosh\mu_{L}d/2}\mathbf{e}_{y}\right)\\&=&-\frac{B_{0}}{\mu_{0}}\frac{\mu_{\mathrm{L}}\sinh\mu_{\mathrm{L}}z}{\cosh\mu_{L}d/2}\mathbf{e}_{x}\ \mathrm{for}\ \left|z\right|\leq d/2\ .\end{eqnarray*}\]
\[\begin{eqnarray*}\nabla\times\mathbf{B}\left(\mathbf{r}\right)&=&\mu_{0}\mathbf{j}_{\mathrm{cond}}\left(\mathbf{r}\right)\ ,\ \mathrm{so}\\\mathbf{j}_{\mathrm{cond}}\left(\mathbf{r}\right) & = &\frac{B_{0}}{\mu_{0}}\nabla\times\left(\frac{\cosh\mu_{\mathrm{L}}z}{\cosh\mu_{L}d/2}\mathbf{e}_{y}\right)\\&=&-\frac{B_{0}}{\mu_{0}}\frac{\mu_{\mathrm{L}}\sinh\mu_{\mathrm{L}}z}{\cosh\mu_{L}d/2}\mathbf{e}_{x}\ \mathrm{for}\ \left|z\right|\leq d/2\ .\end{eqnarray*}\]
So we find that the current is strongest at the termination of the superconducter and vanishing in the middle. Furthermore it has only a component in x-direction, parallel to the surface of the superconductor effectively pushing charges perpendicular to the magnetic field. Of course there is no such thing as an infinitely extended superconductor but we may still get a feeling what happens if the geometry changes.
Assuming a superconducting wire, the current would flow along the radial termination with a negative sense of rotation with respect to the magnetic field effectively pushing it out of the material, see figure. This is different to a perfect diamagnet where the magnetic field in- and outside of the material just remain unchanged if one could somehow turn off the material's resistance.