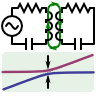
Detuning in Coupled Oscillatory Circuits
Tags: Harmonic Oscillator / Coupling / Resistance / Inductance / Capacitance
Coupled RLC circuits are solved as coupled harmonic oscillators. The detuning of the circuits is calculated.
We have seen how Maxwell's equations can be reduced to explain electro- and magnetostatic phenomena. In the employed descriptions, electric and magnetic field are independent of each other. In electrostatics we assumed a curl-free electric field, \(\nabla\times\mathbf{E}\left(\mathbf{r}\right)=0\). This equation is now replaced by the so-called Maxwell-Faraday equation \[\nabla\times\mathbf{E}\left(\mathbf{r},t\right) = -\partial_{t}\mathbf{B}\left(\mathbf{r},t\right)\ \]whereas the other equations, \(\nabla\cdot\mathbf{E}\left(\mathbf{r},t\right)=\rho\left(\mathbf{r},t\right)/\varepsilon_{0}\), \(\nabla\times\mathbf{B}\left(\mathbf{r},t\right)=\mu_{0}\mathbf{j}\left(\mathbf{r},t\right)\) and \(\nabla\cdot\mathbf{B}\left(\mathbf{r},t\right)=0\) remain unchanged with respect to an explicit time dependency. Please note that we do not work with the full Maxwell eqquations yet. This version is often termed the slowly varying fields approximation of Maxwell's equations and neglects radiation contributions. This formulation is nevertheless extremely useful. Employing the modularization of electrical engineering boiling down electrodynamics to the interaction of the three basic passive elements resistor, capacitor, we will be able to understand a lot of basic phenomena. Thus, we will have a good starting point for more involved circuit theory aspects and a decent starting point for full electrodynamics.

Coupled RLC circuits are solved as coupled harmonic oscillators. The detuning of the circuits is calculated.
The classic problem of the resistance cube is solved. In addition, variations are outlined such as the C- and RLC-Cube

The serial RLC circuit is solved for dissipation and eigenfrequencies.