Tags: Resonance / Kirchhoff's law / Resistance / Inductance / Capacitance
![]() We will study one of the main problems of circuit theory and find basic concepts. Find out when the time-averaged dissipated power in the circuit is maximal using the phasor notation. Get to know a method to calculate the complex eigenfrequencies of the circuit.
We will study one of the main problems of circuit theory and find basic concepts. Find out when the time-averaged dissipated power in the circuit is maximal using the phasor notation. Get to know a method to calculate the complex eigenfrequencies of the circuit.
Problem Statement
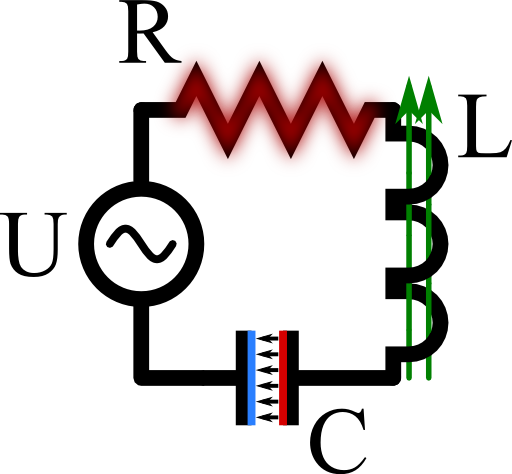 Calculate the time-averaged dissipated power
Calculate the time-averaged dissipated power
\[\left\langle P\left(t\right)\right\rangle =\frac{1}{2\tau}\int_{t-\tau}^{t+\tau}P\left(t\right)dt\]
at the ohmic resistor \(R\) depending on the driving frequency \(\omega_{0}\) of the voltage source,
\[U\left(t\right)=U_{0}\exp\left(-\mathrm{i}\omega_{0}t\right)\]
For which frequency is the dissipation maximal and, physically, why?
Now short the power source and find which relation the impedances have to obey. This relation can also be read as a condition for the complex so-called resonance frequencies / eigenfrequencies \(\omega_{i}\) at which the shortened circuit has to oscillate. Determine the \(\omega_{i}\) and explain their meaning.
Hints
To get the voltage in the complex phasor notation, use
\[\begin{eqnarray*} \delta\left(\omega-\omega_{0}\right)&=&\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{\mathrm{i}\left(\omega-\omega_{0}\right)t}dt\ . \end{eqnarray*}\]
Remember that only real quantities are physical - the present dissipated power at some time \(t\) is given by \(P\left(t\right) = \Re\left[U\left(t\right)\right]\Re\left[I\left(t\right)\right]\).
In time-harmonic dependencies \(\propto\left(-\mathrm{i}\omega_{0}t\right)\) with \(U\left(t\right)=U_{0}e^{-\mathrm{i}\omega_{0}t}+U_{0}^{\star}e^{\mathrm{i}\omega_{0}t}\), \(\Re\left[U\left(t\right)\right]=\frac{1}{2}\left[U\left(t\right)+U^{\star}\left(t\right)\right]\) and likewise for \(I\left(t\right)\),
\[\begin{eqnarray*} P\left(t\right)&=&\frac{1}{4}\left[U_{0}I_{0}^{\star}+U_{0}^{\star}I_{0}\right]+\frac{1}{4}\left[U_{0}I_{0}e^{-2\mathrm{i}\omega_{0}t}+U_{0}^{\star}I_{0}^{\star}e^{2\mathrm{i}\omega_{0}t}\right]\\&=&\frac{1}{2}\Re\left[U_{0}I_{0}^{\star}\right]+\frac{1}{2}\Re\left[U_{0}I_{0}\right]\cos\left(2\omega_{0}t\right)+\frac{1}{2}\Im\left[U_{0}^{\star}I_{0}^{\star}\right]\sin\left(2\omega_{0}t\right)\ . \end{eqnarray*}\]
The time-averaged dissipated power is then given by
\[\begin{eqnarray*} \left\langle P\left(t\right)\right\rangle &=&\frac{1}{2\tau}\int_{t-\tau}^{t+\tau}P\left(t\right)dt\\&=&\frac{1}{2}\Re\left[U_{0}I_{0}^{\star}\right]\ , \end{eqnarray*}\]
since the oscillating terms cancel upon integration.
Let us understand the frequency dependent dissipation in serial RLC circuits now.
At first we may use the complex phasor notation to find power dissipated at the resistor. Then we will determine the resonance frequencies / eigenfrequencies of the circuit.
Dissipation at the Resistor
Kirchhoff's current law implies \(I_{R}\left(t\right)=I_{L}\left(t\right)=I_{C}\left(t\right)\), so
\[\begin{eqnarray*} U\left(t\right)&=&U_{R}\left(t\right)+U_{L}\left(t\right)+U_{C}\left(t\right)\\&=&RI\left(t\right)+L\frac{dI\left(t\right)}{dt}+\frac{1}{C}\int_{.\infty}^{t}I\left(\tau\right)d\tau\ . \end{eqnarray*}\]
A time-differentiation and using the phasor notation yields
\[\begin{eqnarray*} -\mathrm{i}\omega U\left(\omega\right)&=&-\mathrm{i}\omega RI\left(\omega\right)-\omega^{2}LI\left(\omega\right)+\frac{1}{C}I\left(\omega\right)\ ,\\U\left(\omega\right)&=&\left(R-\mathrm{i}\omega L+\frac{\mathrm{i}}{\omega C}\right)I\left(\omega\right)\ ,\ \mathrm{so}\\I\left(\omega\right)&=&\frac{U\left(\omega\right)}{R-\mathrm{i}\omega L+\frac{\mathrm{i}}{\omega C}}\ . \end{eqnarray*}\]
Notice the sign which occurs because of the definition of the Fourier transformation we generally employ on the site:
\[\begin{eqnarray*} U\left(\omega\right)&=&\mathcal{F}\left[U\left(t\right)\right]\left(\omega\right)=\frac{1}{2\pi}\int_{-\infty}^{\infty}U\left(t\right)e^{{\color{red}+}\mathrm{i}\omega t}dt\ . \end{eqnarray*}\]
With the given time-dependent voltage we find
\[\begin{eqnarray*} U\left(\omega\right)&=&\frac{1}{2\pi}\int U\left(t\right)e^{\mathrm{i}\omega t}dt=\frac{U_{0}}{2\pi}\int e^{\mathrm{i}\left(\omega-\omega_{0}\right)t}dt\\&=&U_{0}\delta\left(\omega-\omega_{0}\right)\ . \end{eqnarray*}\]
The current in the phasor notation is likewise given as
\[\begin{eqnarray*} I\left(\omega\right)&=&\frac{U_{0}\delta\left(\omega-\omega_{0}\right)}{R-\mathrm{i}\omega L+\frac{\mathrm{i}}{\omega C}}\ ,\ \mathrm{so}\\I\left(t\right)&=&\int_{-\infty}^{\infty}I\left(\omega\right)e^{-\mathrm{i}\omega t}d\omega\\&=&\frac{U_{0}}{R-\mathrm{i}\omega_{0}L+\frac{\mathrm{i}}{\omega_{0}C}}e^{-\mathrm{i}\omega_{0}t}=I_{0}e^{-\mathrm{i}\omega_{0}t}\ . \end{eqnarray*}\]
This means that the current oscillates with the same frequency as the voltage. Now we can calculate the time-averaged dissipated power as given in the hints as
\[\begin{eqnarray*} \left\langle P_{R}\left(t\right)\right\rangle &=&\frac{1}{2}\Re\left[U_{0}I_{0}^{\star}\right]\\&=&\frac{1}{2}\frac{\left|U_{0}\right|^{2}R}{R^{2}+\left(-\omega_{0}L+1/\omega_{0}C\right)^{2}}\ . \end{eqnarray*}\]
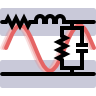
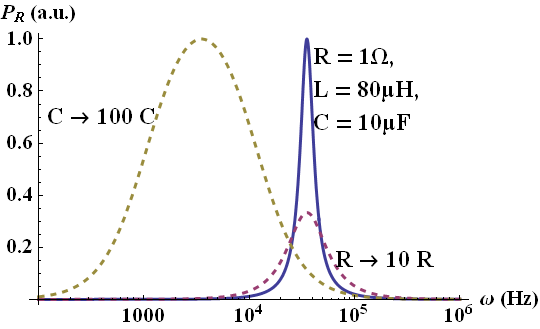 The dissipated power is maximal, if the denominator is minimal. We can directly see that this happens exactly at the (undamped) resonance frequency \(\omega_{r}^{2}=1/LC\) since now the second part in the denominator vanishes. At this frequency, a very strong oscillation between the inductance and capacitance takes places. This strong exchange of energy and charge is accompanied by a maximum current passing through the resistor explaining the dissipation. On the right you can see an example for the dissipation in a certain circuit. Interestingly, an increase in the ohmic resistance decreases \(P_R\) (magenta dotted line). An increase in the capacitance results in a shift to a lower resonance frequency (yellow dotted line).
The dissipated power is maximal, if the denominator is minimal. We can directly see that this happens exactly at the (undamped) resonance frequency \(\omega_{r}^{2}=1/LC\) since now the second part in the denominator vanishes. At this frequency, a very strong oscillation between the inductance and capacitance takes places. This strong exchange of energy and charge is accompanied by a maximum current passing through the resistor explaining the dissipation. On the right you can see an example for the dissipation in a certain circuit. Interestingly, an increase in the ohmic resistance decreases \(P_R\) (magenta dotted line). An increase in the capacitance results in a shift to a lower resonance frequency (yellow dotted line).
Eigenfrequencies
Let us now find the eigenfrequencies \(\omega_{i}\) of the circuit. Those can be thought of as the frequencies at which the circuit would oscillate without any external driving given some initial state, i.e. \(I\left(t\right)=\sum_{i}I_{0,i}\exp\left(-\mathrm{i}\omega_{i}t\right)\).
Using Kirchhoff's laws again, we find
\[\begin{eqnarray*} I_{R}=I_{C}=I_{L}\equiv I&\mathrm{and}&0=U_{R}+U_{C}+U_{L}\ . \end{eqnarray*}\]
This implies
\[\begin{eqnarray*} 0&=&I\left(R-\mathrm{i}\omega L+\frac{\mathrm{i}}{\omega C}\right)\end{eqnarray*}\]
for the inductances. Assuming that the circuit is in some initial state losing energy with complex eigenfrequency \(\omega=\omega^{\prime}+\mathrm{i}\omega^{\prime\prime}\),
\[\begin{eqnarray*} 0&=&\omega R-\mathrm{i}\omega^{2}L+\frac{\mathrm{i}}{C}\ ,\ \mathrm{so}\\\omega_{1,2}&=&\pm\sqrt{\frac{1}{LC}-\left(\frac{R}{2L}\right)^{2}}-\mathrm{i}\frac{R}{2L}\ . \end{eqnarray*}\]
We get two solutions with real parts of opposite sign that are lowered with respect to the undamped resonance frequency. Furthermore, we find that \(\omega^{\prime\prime}=-R/2L\). This corresponds to a damping constant since \(\exp\left(-\mathrm{i}\omega t\right)=\exp\left(-\mathrm{i}\omega^{\prime}t+\omega^{\prime\prime}t\right)\). Fortunately we found the correct sign in the imaginary part of the eigenfrequencies - otherwise the amplitude of the undriven circuit would grow in time...