Radiation of an Electron on a Radial Path: The Larmor Formula

We calculated the radiation of an electron on a radial path. Delve into the intricate relationship between motion, acceleration, and radiation, and discover the profound implications of this phenomenon in fields ranging from accelerator physics to astrophysics.

Motivation

The dance of an electron around a nucleus, or in any path dictated by external forces, is more than a mere movement; it's a ballet that bridges the classical world of physics with the quantum realm. When an electron accelerates, as it does on a radial path, it emits radiation, a phenomenon that sits at the heart of understanding not only the electromagnetic spectrum but also the very fabric of particle physics. This exploration into the radiation of an electron on a radial path is not just an academic exercise ↗↗. It is a journey that connects the dots between Maxwell's electromagnetic theory and the nuances of quantum electrodynamics, offering insights into the behavior of charged particles under acceleration.

The motivation behind unraveling this problem is manifold. It not only illuminates the fundamental principles of electromagnetic radiation but also underscores the pivotal role of acceleration in generating radiation. For students and professionals in the fields of physics and engineering, mastering these concepts paves the way for innovations in accelerator physics ↗, astrophysics, and the development of radiation sources for medical and industrial applications. Beyond its practical implications, this problem enhances critical thinking and problem-solving skills, essential for the physicists and engineers of tomorrow who aim to push the boundaries of what's possible in technology and science.

Problem Description

Imagine an electron, that tiny bastion of charge, moving radially in a uniform circular motion with a constant angular velocity (\omega) ↗ ↗. This motion, while simple in its uniformity, requires a centripetal acceleration to maintain the electron's circular path. This acceleration, in turn, causes the electron to emit radiation, a fascinating phenomenon that we aim to quantify.

For the simplicity of our problem, let's assume the electron does not lose energy and thus maintains its velocity. Our goal is to calculate the power radiated by the electron due to its acceleration. The expected outcome is an expression for the power radiated by the electron, intertwining its acceleration with fundamental constants of nature.

Hints

Before diving into the solution, let's arm ourselves with a couple of crucial hints. First, recall the Larmor formula, which provides the power radiated by a non-relativistic accelerating charge as

\[P = \mu_0 \frac{q^2a^2}{6 \pi c}\]

where \(q\) is the charge, \(a\) is the acceleration, and \(c\) is the speed of light. For circular motion, the centripetal acceleration \(a\) is given by \(a = r\omega^2\), where \(r\) is the radius of the circle and \(\omega\) is the angular velocity. These pieces of information will be instrumental in our solution.

You will see that finding the solution becomes pretty easy knowing Larmor's formula. In the appendix we have assembled some hints on how to derive the Larmor formula.

Solution

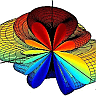
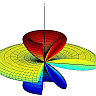
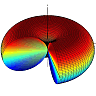
Let's embark on solving this intriguing problem. We start by acknowledging that the electron emits radiation due to its centripetal acceleration in circular motion. The Larmor formula comes into play here, given as:

\[P = \mu_0 \frac{q^2a^2}{6 \pi c}\]

The electron's charge \(q\) is a known constant (\(q = -e\)), and \(c\) is the speed of light. The centripetal acceleration \(a\), pivotal to our calculation, is expressed in terms of the electron's angular velocity \(\omega\) and the radius of its circular path \(r\), as \(a = r\omega^2\).

Substituting the expression for \(a\) into the Larmor formula, we get:

\[P = \mu_0 \frac{e^2r^2\omega^4}{6 \pi c}\]

This result is profound. It reveals how the power radiated increases with the fourth power of the angular velocity (\(\omega^4\)) and the square of the radius (\(r^2\)) of the electron's path.

The journey from the motion of an electron to the radiation it emits is a testament to the beauty and complexity of physics. This problem, rooted in classical electrodynamics, extends its branches into the quantum realm, offering a glimpse into the behavior of charged particles under acceleration.

Understanding such phenomena is not just an academic endeavor. It's a cornerstone for advancements in various fields, from accelerator physics to astrophysics, and plays a crucial role in the development of radiation sources for health and industry. As we stand on the shoulders of giants like Maxwell and delve into the quantum world, we're reminded of the endless possibilities that physics offers to decipher the universe's mysteries and harness its laws for the betterment of humanity.

Background: Road to Derivation of Larmor Formula and its Historical Context

The quest to understand the universe has led humanity to unravel many of its mysteries, one of which is electromagnetic radiation. This phenomenon is not just a cornerstone of modern physics but also a foundation upon which much of today's technology is built. From the radio waves that carry our conversations across vast distances, to the X-rays that peer into the human body, electromagnetic radiation shapes our world in countless ways. At the heart of our understanding of this critical phenomenon lies the work of Joseph Larmor, a physicist whose contributions have had a lasting impact on both theory and application.

Joseph Larmor, born in 1857, was a mathematician and physicist who sought to explain how an accelerating charge emits electromagnetic radiation. His work, encapsulated in what is now known as the Larmor formula, provides a mathematical description of the power radiated by an accelerating charged particle. This breakthrough was not just a significant achievement in its own right; it also paved the way for the development of quantum mechanics and modern physics, influencing giants in the field such as Hendrik Lorentz and Albert Einstein.

The Larmor formula remains highly relevant for undergraduate and graduate students of physics today, finding applications in diverse areas such as antenna theory, radiation therapy, and astrophysics. This article embarks on a journey from the historical context of Larmor's work to the mathematical derivation of his famous formula. Along the way, we will explore the interplay between historical events, such as the industrial revolution, and the development of electromagnetic theory, offering a multidisciplinary exploration of a topic that continues to fascinate and challenge physicists around the world.

Historical Context and Larmor's Contribution

Before Joseph Larmor's seminal contribution, the landscape of electromagnetic theory was dominated by James Clerk Maxwell's equations. These equations, formulated in the mid-19th century, described how electric and magnetic fields interact but left unanswered questions about the nature of electromagnetic radiation from accelerating charges. The late 19th and early 20th centuries, a period marked by the second industrial revolution, provided a fertile ground for scientific inquiry, driven by technological advancements and a burgeoning interest in the fundamental laws of nature.

It was within this vibrant scientific environment that Larmor, along with contemporaries like Hendrik Lorentz and later Albert Einstein, sought to deepen the understanding of electromagnetic phenomena. The specific challenge they faced was understanding how and why accelerating charges emit radiation, a question that had implications far beyond the confines of theoretical physics, touching upon the design of electrical machinery, the nature of light, and the structure of the atom.

Larmor's interests in both mathematics and physics uniquely positioned him to tackle this problem. In 1897, he published his findings, introducing the world to what would become known as the Larmor formula. This formula, often expressed in cgs units, reads:

\[P = \frac{2}{3}\frac{q^2a^2}{c^3}\]

The formula quantified the power radiated by an accelerating charged particle, linking it to the charge's acceleration and the speed of light. The initial reception within the scientific community was one of intrigue and curiosity, as Larmor's work offered a new lens through which to view the behavior of electromagnetic fields and radiation.

The significance of Larmor's formula extended far beyond its immediate implications for electromagnetic theory. It served as a precursor to more comprehensive theories in electromagnetism and quantum mechanics, laying the groundwork for the development of special relativity by Albert Einstein and the electron theory by Hendrik Lorentz. Larmor's work demonstrated the power of mathematical physics to unlock the secrets of the natural world, a legacy that continues to inspire and inform the study of physics today.

Guide do the Derivation of the Larmor Formula

The Larmor formula, a cornerstone in the field of electromagnetism, provides a quantitative description of the power radiated by an accelerating charge ↗. The journey to its derivation begins with the foundational principles of electromagnetic theory, particularly focusing on the behavior of accelerating charges and their relationship with electromagnetic radiation.

At the heart of this exploration are Maxwell's equations, which describe how electric \(\mathbf{E}\) and magnetic \(\mathbf{B}\) fields are generated by charges and currents, and how they propagate through space. For the derivation of the Larmor formula, the key principle is that an accelerating charge emits electromagnetic radiation, which carries energy away from the charge.

Here's the approach for the derivation of the formula:

Accelerating Charge and Maxwell's Equations: Consider a charge *q* undergoing acceleration *a*. According to electromagnetic theory, this acceleration results in the emission of electromagnetic radiation. The electric \(\mathbf{E}\) and magnetic \(\mathbf{B}\) fields generated by this accelerating charge can be described by Maxwell's equations.

Maxwell's equations in free space, in differential form, are: \[\nabla \cdot \mathbf{E} = 0, \quad \nabla \cdot \mathbf{B} = 0\] \[\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}, \quad \nabla \times \mathbf{B} = \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t}\] where \(\nabla \cdot\) and \(\nabla \times\) are the divergence and curl operators, respectively, \(\mu_0\) is the permeability of free space, and \(\varepsilon_0\) is the permittivity of free space.

Retarded Potentials: To solve Maxwell's equations for the fields \(\mathbf{E}\) and \(\mathbf{B}\) generated by an accelerating charge, we introduce the concept of retarded potentials, \(\Phi\) and \(\mathbf{A}\), which account for the finite speed of light. They are given by: \[ \Phi(\mathbf{r}, t) = \frac{1}{4\pi\epsilon_0}\frac{q}{|\mathbf{r} - \mathbf{r'}|} \Bigg|_{t' = t - \frac{|\mathbf{r} - \mathbf{r'}|}{c}} \] \[ \mathbf{A}(\mathbf{r}, t) = \frac{\mu_0}{4\pi}\frac{q\mathbf{v'}}{|\mathbf{r} - \mathbf{r'}|} \Bigg|_{t' = t - \frac{|\mathbf{r} - \mathbf{r'}|}{c}} \] where \(\mathbf{r}\) is the observation point, \(\mathbf{r'}\) and \(\mathbf{v'}\) are the position and velocity of the charge at the retarded time \(t'\).

Electric and Magnetic Fields: The electric and magnetic fields can be expressed in terms of the retarded potentials: \[ \mathbf{E} = -\nabla\Phi - \frac{\partial \mathbf{A}}{\partial t}, \quad \mathbf{B} = \nabla \times \mathbf{A} \]

Radiated Power Calculation: The power \(P\) radiated by the charge can be calculated by integrating the Poynting vector \(\mathbf{S} = \frac{1}{\mu_0} (\mathbf{E} \times \mathbf{B})\) over a sphere surrounding the charge. The Poynting vector represents the directional energy flux (or power per unit area) of an electromagnetic field.

Expression for \(P\): The calculation of the radiated power \(P\) involves some complex vector calculus and approximations for the far field:

Vector Calculus: The Poynting vector \(\mathbf{S}\) is given by \(\mathbf{S} = \frac{1}{\mu_0} (\mathbf{E} \times \mathbf{B})\), which is a cross product of the electric and magnetic fields. The power \(P\) radiated by the charge is then given by the integral of the Poynting vector over a sphere surrounding the charge, which involves the divergence theorem. The divergence theorem is a fundamental result in vector calculus that relates the flux of a vector field through a closed surface to the divergence of the field in the volume enclosed by the surface. In this case, it allows us to calculate the total power radiated by the charge.

Far-Field Approximations: The calculation of the radiated power \(P\) involves approximations for the far field. In the far field (or radiation zone), the distance from the source is much greater than the wavelength of the radiation. Under this approximation, the electric and magnetic fields can be simplified, and the terms involving the charge's velocity can be neglected compared to those involving its acceleration. This is because the radiation is primarily due to the charge's acceleration, not its velocity.

Retarded Time Approximation: Another approximation involves the retarded time. The fields are evaluated at the retarded time \(t' = t - \frac{|\mathbf{r} - \mathbf{r'}|}{c}\), which accounts for the time it takes for the radiation to reach the observer. For an observer very far from the charge (in the far field), the difference between the retarded time and the present time is negligible, so the fields can be evaluated at the present time. \[ P = \frac{2}{3}\frac{q^2a^2}{c^3} \mathrm{cgs\ units}\]

This equation, known as the Larmor formula, succinctly captures the essence of electromagnetic radiation from an accelerating charge. Note again that the formula is given in cgs units. The reason is that these units are often used in relativistic electrodynamics, see for example the more detailled derivation of the Larmor formula on Wikipedia.

Implications and Applications

The Larmor formula is not just a theoretical construct; it has profound implications and applications across various fields of physics, shedding light on phenomena from the microscopic to the cosmic.

Quantum Electrodynamics (QED): The Larmor formula plays a pivotal role in the development of QED, the quantum theory that describes how light and matter interact. It provides a classical limit that QED must reduce to, for phenomena involving low energies and large distances compared to atomic scales.
Astrophysics: In astrophysics, the Larmor formula is instrumental in understanding the radiation mechanisms of pulsars and other celestial objects. The intense electromagnetic radiation emitted by these objects can often be traced back to accelerating charges in their magnetic fields, with the Larmor formula providing a quantitative measure of this radiation.
Medical Physics: In the realm of medical physics, particularly in radiation therapy for cancer treatment, the Larmor formula helps in calculating the dose of radiation emitted by charged particles as they decelerate upon interacting with matter. This is crucial for targeting cancer cells while minimizing damage to surrounding healthy tissues.
Technology: The principles encapsulated in the Larmor formula are applied in the design of antennas and accelerators. Antennas, for instance, radiate electromagnetic waves by accelerating electrons, and the efficiency of this radiation can be optimized using insights from the Larmor formula.
Limitations and Relativistic Corrections: While the Larmor formula provides a robust framework for understanding electromagnetic radiation from accelerating charges, it has its limitations, particularly when relativistic effects become significant. For charges moving at speeds close to the speed of light, relativistic corrections are necessary to accurately describe the radiation.
Ongoing Research: The Larmor formula continues to inspire research in physics, from exploring its quantum mechanical analogs to studying its implications in high-energy astrophysics and beyond. Its simplicity and generality make it a powerful tool for investigating new phenomena.
Educational Value: For physics students, the Larmor formula serves as a bridge between classical electromagnetism and modern physics, illustrating how fundamental principles can lead to profound insights into the natural world.

The enduring legacy of Joseph Larmor and the formula that bears his name underscore the continued relevance of his contributions to both theoretical and applied physics ↗. As we unravel the mysteries of the universe, from the quantum to the cosmic, the Larmor formula remains a beacon of understanding, guiding the way forward.