Tags: Rotational Symmetry / Near Field / Far Field
![]() To have a certain solution at hand is often useful construct another one out of it. This is the case for the electrostatic potential and field of the charged ring that can be generalized to the homogeneously charged disk and cylinder. Find out how to calculate the solutions on the axis of symmetry.
To have a certain solution at hand is often useful construct another one out of it. This is the case for the electrostatic potential and field of the charged ring that can be generalized to the homogeneously charged disk and cylinder. Find out how to calculate the solutions on the axis of symmetry.
Problem Statement
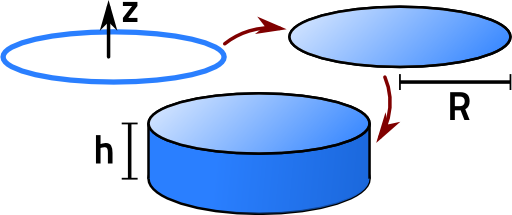
To calculate the electrostatic potential and electric field of a disk, it is useful to follow a two-step procedure as seen below. Unfortunately, the involved integrals would become incredibly complicated if we would not restrict ourselves to the z-axis of symmetry. In the end we will see how we can use the results for the disk to find the field of a cylinder - up to some technical steps.
- Derive the electric field Ering(r) of a uniformly charged ring with radius R along the z-axis.
- Use your result for the ring charge to calculate the electric field Edisk(r) of a uniformly charged disk with radius R, also along the z-axis. Discuss the limiting cases z ≪ R (near field) and z ≫ R (far field).
- Write down the equation that you would use to calculate the electrostatic potential ϕring(r) of a uniformly charged cylinder with radius R and height h. Restrict yourself even in this general approach to the axis of symmetry.
Hints
Consider the disk as a summation of rings with increasing radii.
Mathematically, the charge distribution of a ring charge with radius R is given by
\[\rho_{\mathrm{\, ring}}\left(\mathbf{r}\right) = \eta\delta\left(z\right)\delta\left(\varrho-R\right)\ .\]
Here, η is the charge density per unit length.
Note that the symmetry of each individual charge distribution is rotational symmetry. In this case a movement around the z-axis does not change the body.
Solution
First we will calculate the electrostatic potential ϕring(r)of the charged ring and then derive its corresponding electric field Ering(r). We will then get the disk-potential ϕdisk(r) by integrating the ring-solution for different radii. At last we will write down how to get the equation for calculating the electric potential ϕcylinder(r) of a homogenously charged cylinder.
Electrostatic Potential Of A Uniformly Charged Ring
We calculate the electrostatic potential ϕring(r) similar to that of the line charge. Because of the obvious rotational symmetry of the problem, we switch to cylindric coordinates and use the ring charge distribution:
\[\rho_{\mathrm{\, ring}}\left(\mathbf{r'}\right)=\eta\delta\left(z'\right)\delta\left(\varrho'-R\right)\]
Here, R is the radius of the ring:
\[\begin{eqnarray*} \phi_{\,\mathrm{ring}}\left(\mathbf{r}\right)&=&\frac{1}{4\pi\varepsilon_{0}}\int\frac{\rho\left(\mathbf{r'}\right)}{|\mathbf{r-r'}|}dV'\\&=&\frac{1}{4\pi\varepsilon_{0}}\iiint\frac{\eta\delta\left(z'\right)\delta\left(\varrho'-R\right)}{|\mathbf{r-r'}|}\varrho'd\varrho'd\varphi'dz'\\&=&\frac{\eta}{4\pi\varepsilon_{0}}\intop_{0}^{2\pi}\frac{R}{|\mathbf{r}-R\cdot\mathbf{e}_{\varrho}^\prime|}d\varphi', \end{eqnarray*}\]
In general, the distance between r and R·eρ' results in integrals we may not determine in simple functions. On the z axis of symmetry, however, this difference is simply given by
\[ | z \mathbf{e}_z - R \mathbf{e}_{\varrho}^{\prime}| = \sqrt{z^{2}+R^{2}}\ .\]
Now the integral is quite easy and we get for the ring-potential
\[\phi_{ring}\left(\mathbf{r}\right) = \frac{2\pi \eta }{4\pi\varepsilon_{0}}\cdot\frac{R}{\sqrt{z^{2}+R^{2}}} \ . \]
To obtain the electric field, we have to calculate ∂φ/∂z. We find
\[\mathbf{E}_{\,\mathrm{ring}}\left(\mathbf{r}\right)=-\frac{\eta}{2\varepsilon_{0}}\frac{zR}{\left|z^{2}+R^{2}\right|^{3}}\ .\]
Electrostatic Potential Of A Uniformly Charged Disk
Now twe know the electrostatic potential of a ring, ϕring(r). We can use our finding to calculate the potential of a uniformly charged disk. We can imagine the charged disk to be a summation over infinitely many charged rings. In mathematical terms, we just have to integrate over the radius R:
\[\begin{eqnarray*} \phi_{\,\mathrm{disk}}\left(z\right)&=&\frac{1}{4\pi\varepsilon_{0}}\iiint\frac{\eta\delta\left(z'\right)}{|z\mathbf{e}_z-\varrho'\mathbf{e}_\varrho^\prime|}\varrho'd\varrho'd\varphi'dz'\\&=&\frac{1}{4\pi\varepsilon_{0}}\intop_{0}^{2\pi}\intop_{0}^{R}\frac{\eta}{|z\mathbf{e}_z-\varrho'\mathbf{e}_\varrho^\prime|}\varrho'd\varrho'd\varphi'\\&=&\frac{2\pi}{4\pi\varepsilon_{0}}\intop_{0}^{R}\frac{\eta}{\sqrt{z^{2}+\varrho'^{2}}}\varrho'd\varrho' \end{eqnarray*}\]
To solve this integral, we may use a standard substitution:
\[\begin{eqnarray*}u&=&z^{2}+\varrho'^{2}\ ,\mathrm{with} \\ \frac{du}{d\varrho'}&=&2\varrho'\ . \end{eqnarray*}\]
Now we may solve the integral:
\[\begin{eqnarray*} \phi_{\,\mathrm{disk}}\left(z\right)&=&\frac{1}{4\varepsilon_{0}}\intop_{z^{2}}^{z^{2}+R^{2}}\frac{\eta}{\sqrt{u}}du\\&=&\frac{\eta}{2\varepsilon_{0}}\left(\sqrt{z^{2}+R^{2}}-|z|\right) \end{eqnarray*}\]
Yet again, the electric field results from a \(z\)-derivation of the potential. The calculation is is not extremely involved and we find
\[\mathbf{E}_{\,\mathrm{disk}}\left(z\right)=-\frac{\eta}{2\varepsilon_{0}}\left[\frac{z}{\sqrt{z^{2}+R^{2}}}-\mathrm{sqn(z)}\right]\ ,\]
Here, "sgn" is the function that indicates the sign of its argument. In principle we have everything at hand to deduce the solution for a homogeneously charged cylinder. Just because we have just one symmetry in the system makes the integration too technical to be shown here.
A related, more symmetric and thus analytically solvable (in terms of basic functions) problem is "the electric field and potential of a homogeneously charged sphere".
Electrostatic Potential Of A Uniformly Charged Cylinder
The calculation of the electrostatic potential of a uniformly charged cylinder involves some nasty integrals. We will be happy to write down the solution on the axis of symmetry in terms of those integrals without solving them. Naturally, we would have to integrate our disk solution along new positions.
Assuming that the cylinder is placed symmetrically from z = -h/2 to z = h/2, we find
\[\begin{eqnarray*} \phi_{\,\mathrm{cylinder}}\left(z\right)&=&\frac{\eta}{2\varepsilon_{0}}\intop_{-\frac{h}{2}}^{\frac{h}{2}}\left[\sqrt{\left(z-z'\right)^{2}+R^{2}}-|z-z'|\right]dz' \end{eqnarray*}\ .\]
Disk Potential in the Near and Far Field Limits
There are two more interesting cases to look at. First, what will happen if we look from a very big distance at our charged object and z ≫ R (far field) and second, what happens if the radius R is very big compared to the position from where we look at the object z ≪ R (near field).
Ring-Potential
First let's see, what will happen with our ring-potential if we look from a very big distance at it - the far field limit. Herefore we look at z → ∞. We get with
\[2\pi \eta R = q\]
\[\begin{eqnarray*} \phi_{\,\mathrm{ring}}\left(z\right)&=&\frac{q}{4\pi\varepsilon_{0}}\cdot\frac{1}{\sqrt{z^{2}+R^{2}}}\\&=&\frac{q}{4\pi\varepsilon_{0}}\cdot\frac{1}{z\sqrt{1+\left(\frac{R}{z}\right)^{2}}} \end{eqnarray*}\]
Now we may consider the Taylor expansion
\[\sqrt{1+x}\approx1+\frac{1}{2}x^{2}+O\left(x^{3}\right)\]
to find
\[\phi_{\,\mathrm{ring}}\left(z\right)\approx\frac{q}{4\pi\varepsilon_{0}}\cdot\frac{1}{z\cdot\left(1+\frac{1}{2}\left(\frac{R}{z}\right)^{2}\right)}\]
In the limit of \(z\rightarrow\infty\) we can see that
\[ \phi_{\,\mathrm{ring}}\left(\mathbf{r}\right)\approx\frac{q}{4\pi\varepsilon_{0}}\cdot\frac{1}{z}.\]
Which, of course, looks like the electric field of a point charge.
Now let us take a look at the near field case, where z ≪ R:
\[\begin{eqnarray*} \phi_{\,\mathrm{ring}}\left(z\right)&=&\frac{\eta R}{2\varepsilon_{0}}\cdot\frac{1}{\sqrt{z^{2}+R^{2}}}\\&=&\frac{\eta R}{2\varepsilon_{0}}\cdot\frac{1}{R\sqrt{1+\left(\frac{z}{R}\right)^{2}}} \end{eqnarray*}\]
We can directly see that in the limit of R → ∞
\[\phi_{\,\mathrm{ring}}\left(z\right) \rightarrow \frac{\eta}{2\varepsilon_0}\ ,\]
a result that may seem surprising at first. However, if we look at the field of a homogeneously charged sphere, we may recognize that the surrounding charges are effectively pushing the potential to some constant value at the origing.
Disk-Potential
Analogous to the charged ring-potential, we consider the far- and nearfield limits with z ≫ R and z ≪ R.
Like before we first consider here the farfield case z ≫ R. Without any loss of generality, we may assume that z ≥ 0:
\[\begin{eqnarray*} \phi_{\,\mathrm{disk}}\left(z\right)&=&\frac{\eta}{2\varepsilon_{0}}\left(\sqrt{z^{2}+R^{2}}-|z|\right)\\&=&\frac{\eta}{2\varepsilon_{0}}\cdot z\left(\sqrt{1+\left(\frac{R}{z}\right)^{2}}-1\right) \ ,\ \mathrm{for}\ z\gt 0 \\&\approx&\frac{\eta}{2\varepsilon_{0}}\cdot z\left(1+\frac{1}{2}\left(\frac{R}{z}\right)^{2}-1\right)\\ &\rightarrow&\frac{\eta R}{4\varepsilon_{0}}\cdot\frac{R}{z} \end{eqnarray*}\]
Again a result that looks, unsurprisingly, quite similar to the potential of a point charge.
Now the nearfield limit of the charged disk with z ≪ R:
\[\begin{eqnarray*} \phi_{\,\mathrm{disk}}\left(z\right)&=&\frac{\eta}{2\varepsilon_{0}}\left(\sqrt{z^{2}+R^{2}}-|z|\right)\\ &=&\frac{\eta}{2\varepsilon_{0}}\cdot\left(R\sqrt{1+\left(\frac{z}{R}\right)^{2}}-\left|z\right|\right)\\ &\rightarrow&\frac{\eta}{2\varepsilon_{0}}\cdot\left(R-\left|z\right|\right) \end{eqnarray*}\]
The potential we have just determined is that of homogeneously charged half plane with constant electric field. The different limiting cases are shown in the figure below:
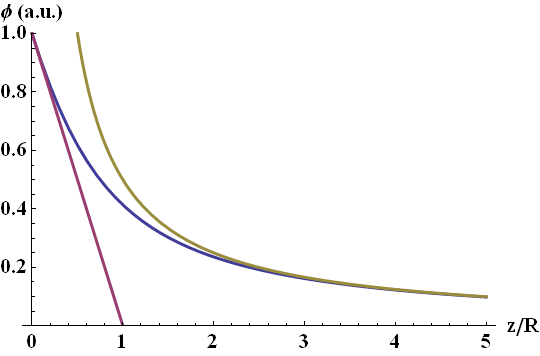
Near and field limits of the electrostatic potential of a homogeneously charged disk: magenta and yellow lines.
The correct solution (blue line) on the z axis of symmetry is matched by the approximative solutions for small and big z.
I hope that this solution was interesting for you! We have seen how different integral and limiting approaches yield to physically interesting results. Also, in the far field we encountered once more that the charge looked like a point like one. Have you noticed how the rotational symmetry of the problem made it solvable?