Tags: Far Field / Directivity / Poynting Vector / Dipole / Radiation pattern
![]() One of the most widely used antennas in telecommunication is the dipole antenna. In this problem, we investigate the radiation properties of such an antenna. We first calculate the electromagnetic fields far away from the antenna. Then, as a special cases we discuss half-wavelength, full-wavelength and larger dipole antennas.
One of the most widely used antennas in telecommunication is the dipole antenna. In this problem, we investigate the radiation properties of such an antenna. We first calculate the electromagnetic fields far away from the antenna. Then, as a special cases we discuss half-wavelength, full-wavelength and larger dipole antennas.
As the name suggests, a dipole antenna consist of two terminals (poles), where the radio frequency current is applied by a transmitter or extracted by a receiver. One of the simplest form of dipole antennas consist of two pieces of straight and thin metallic wire, which are oriented on a common axis.
Generally, each of these wires may have different lengths depending on the application. Below an image of such an antenna is shown. In one special case the lengths of both wires are equal to one forth of the wavelength of the radiating wave. Therefore, the length of the whole antenna is equal to half of the wavelength. Thus, this antenna is called half-wave dipole antenna. For the infinitesimal dipole please regard a corresonding worksheet.
Problem Statement
A symmetric and very thin dipole antenna which works at frequency ω is placed in a homogeneous environment with permitivity and permeability of ε and μ. It can be shown that the antenna has approximately the following current distribution.
where, l = 0 is the current amplitude at the feed point of the antenna, k = 2π/λ, λ is the wavelength of the radiating wave, l is the total length of the antenna, δ(ρ) is delta function, ρ is the radial distance from the z axis in cylindrical coordinate, and ez is the unit vector in z direction.
- Find the far field electric and magnetic fields E(r,ω), H(r,ω) generated by the antenna.
- Approximate your results for \(l\ll\lambda\) and compare them to the results of "The Infinitesimal Dipole". In this case, calculate the radiation resistance of the antenna.
- Sketch approximately the far filed radiation pattern in principal planes for
- Half-wave dipole antenna (\(l=\lambda / 2\))
- Full-wave dipole antenna (\(l=\lambda\))
- Somewhat larger antenna, \(l=1.4\lambda\) and
- \(l=1.5\lambda\)
Hints
In "The Infinitesimal Dipole" it is shown that for an infinitesimal antenna with current distribution of
\[\mathbf{J}\left(\mathbf{r},\omega\right)=J_0 \, \delta (\mathbf{r})\, \mathbf{e}_z\]
the vector potential is given by \[\mathbf{A}(\mathbf{r},\omega)=\frac{\mu\,J_0}{4\pi}\,\frac{ e^{\mathrm{i} k r}}{r}\,\mathbf{e}_z\]
Think of an arbitrary antenna as a collection of many infinitesimal antennas, and try to extend this formula to find the vector potential of the dipole antenna.
Radiation resistance \(R_a\) is defined as below:
\[P_r=\frac{1}{2} I_0^2 R_a\]
where, \(P_r\) is the total radiated power by the antenna and \(I_0\) is feed point current amplitude.
Principal planes are defined as below:
- Principal E-plane which includes the direction of maximum radiation and the electric field.
- Principal H-plane which includes the direction of maximum radiation and the magnetic field.
Okay, let us move on to find the solution for the finite dipole antenna.
1. Far Field Determination
In this part we first generalize our findings in "The Infinitesimal Dipole" to an arbitrary current distribution. In other words, we want to find the vector potential \(\mathbf{A}(\mathbf{r},\omega)\) for an arbitrary current distribution \(\mathbf{J}\left(\mathbf{r'},\omega\right)\). And, to do that we use the results of "The Infinitesimal Dipole".
The linearity of Maxwell equations and constitutive relations allow us to use the superposition principle. It means that we can decompose the current distribution into arbitrarily number of parts, then calculate the vector potential for each part, and finally add all vector potentials which is equal to the vector potential of the original current distribution.
Based on this fact, the current distribution can be decomposed into infinite infinitesimal current pieces. One of these tiny pieces of current which is located at position \(\mathbf{r'}\) can be written as \(\mathbf{J}\left(\mathbf{r'},\omega\right)dV' \, \delta (\mathbf{r-r'})\), where \(dV'\) is a volume element. Therefore, according to "The Infinitesimal Dipole" the contribution of this infinitesimal current to the total vector potential is \(\frac{\mu\,\mathbf{J}\left(\mathbf{r'},\omega\right)dV'}{4\pi}\,\frac{ e^{\mathrm{i} k |\mathbf{r'-r}|}}{|\mathbf{r'-r}|}\), where \(|\mathbf{r'-r}|\) indicates the distance between the tiny part of current and the observation point. Now, to obtain the total vector potential we need just to add up the contributions of all infinitesimal currents, that is: \begin{equation} \Rightarrow\mathbf{A}(\mathbf{r},\omega)=\int_{V'}\frac{\mu\,\mathbf{J}\left(\mathbf{r'},\omega\right)}{4\pi}\,\frac{ e^{\mathrm{i} k |\mathbf{r'-r}|}}{|\mathbf{r'-r}|} dV' \tag{1}\label{AJ} \end{equation}
In this equation, \(V'\) denotes the volume of the current distribution. Note that equation [\ref{AJ}] is a general formula that can be applied to any current distribution.
Now, one might use equation [\ref{AJ}] to find \(\mathbf{A}(\mathbf{r},\omega)\), then \(\mathbf{E}(\mathbf{r},\omega)\) and \(\mathbf{H}(\mathbf{r},\omega)\), and finally approximate them to find far fields. As you might also noticed, there are some drawbacks in this procedure. First of all, most of the time it is not possible to solve equation [\ref{AJ}] exactly. Second, we do not need to know the exact form of vector potential to find far fields. It is sufficient to know the vector potential for far zone to find far fields. Therefore, it is wise to approximate equation [\ref{AJ}] for far zone.
In reality the distance between antennas are far larger than the dimensions of the antennas themselves, i.e. \(\forall \mathbf{r'} \in V': r\gg r'\). Therefore, one can use this fact to simplify equation [\ref{AJ}]. To do that we can approximate \(|\mathbf{r'-r}|\) in the denominator of the kernel of the integral in equation [\ref{AJ}] by the first term of its Taylor expansion. \begin{equation} \Rightarrow\frac{1}{|\mathbf{r'-r}|}\simeq \frac{1}{r}\quad\quad, r\gg r' \tag{2}\label{Ap1} \end{equation}
However, we cannot use this approximation for the exponent; because the exponential function which pure imaginary argument is a periodic function which varies much faster than the denominator. Therefore, we should use a better approximation for that. Thus, we approximate the exponent by the first two terms of its Taylor expansion: \begin{eqnarray} |\mathbf{r'-r}|&=&\sqrt{r'^2+r^2-2\,r'\,r\,\cos(\theta)}\nonumber\\&=&r-r'\cos(\theta)+\frac{r'^2\sin^2(\theta)}{2r}+...\tag{3}\label{Apr}\\&\simeq & r-r'\cos(\theta)\nonumber\\&=& r-\,\mathbf{r'}.\,\mathbf{e}_r\nonumber \end{eqnarray} \begin{equation} \Rightarrow e^{\mathrm{i} k |\mathbf{r'-r}|} \simeq e^{\mathrm{i} k(r-\,\mathbf{r'}.\,\mathbf{e}_r)}\quad\quad, r\gg r' \tag{4}\label{Ap2} \end{equation} where \(\theta\) is the angle between \(\mathbf{r'}\) and \(\mathbf{r}\), and \(\mathbf{e}_r\) is the unit vector in radial direction.
Now, by substituting equation [\ref{Ap1}] and [\ref{Ap2}] into equation [\ref{AJ}] we obtain: \[\mathbf{A}(\mathbf{r},\omega)\simeq\int_{V'}\frac{\mu\,\mathbf{J}\left(\mathbf{r'},\omega\right)}{4\pi}\frac{ e^{-\mathrm{i} k\, (r-\mathbf{r'}.\,\mathbf{e}_r)}}{r} dV'\] \begin{equation} \Rightarrow\mathbf{A_{ff}}(\mathbf{r},\omega)=\frac{\mu\,e^{\mathrm{i} k r}}{4\pi r}\int_{V'}\mathbf{J}\left(\mathbf{r'},\omega\right) e^{-\mathrm{i} k\, \mathbf{r'}.\,\mathbf{e}_r}dV' \tag{5}\label{Aff} \end{equation} Equation [\ref{Aff}] gives us the far zone vector potential. And, we will use it as the fundamental formula in almost all problems related to antennas.
Now, we need to know the conditions under which our approximation is valid which defines the far field zone. To obtain equation [\ref{Aff}] from equation [\ref{AJ}] we used two approximations: one in the exponent and one in the denominator of the kernel of the integral. The impact of our approximation for the denominator is negligible in comparison to the approximation of the exponent; because, \(e^{\mathrm{i} k |\mathbf{r'-r}|}\) varies much faster than \(\frac{1}{|\mathbf{r'-r}|}\) for \(r\gg r'\). Therefore, we only consider the error introduced to \(\mathbf{A}(\mathbf{r},\omega)\) by approximating the exponent.
It has been shown by numerical and experimental tests that when the maximum error in the exponent is smaller than \(\frac{\pi}{8}\), the approximation for vector potential is acceptable and \(\mathbf{A_{ff}}(\mathbf{r},\omega)\) gives good results. According to equation [\ref{Apr}], the most significant neglected term in approximating the exponent is \(k\frac{r'^2\sin^2(\theta)}{2r}\). Therefore the maximum error is equal to \(k\frac{r'^2_{max}}{2r}\) (when \(\theta=\frac{\pi}{2}\) and \(r'\) is maximum). Thus: \[k\frac{r'^2_{max}}{2r} < \frac{\pi}{8}\; \Rightarrow\frac{2\pi}{\lambda}\frac{r'^2_{max}}{2r} < \frac{\pi}{8} \Rightarrow \frac{8 r'^2_{max}}{\lambda} < r\ , \mathrm{so} \]
\begin{equation} \frac{2L^2}{\lambda} < r \tag{6}\label{ff} \end{equation} in which \(L=2r_{amx}\) is the largest dimension of the antenna. Equation [\ref{ff}] determines the far zone for an antenna with largest dimension of \(L\). Therefore, equation [\ref{Aff}] is valid as far as equation [\ref{ff}] is satisfied, which is the case for most practical applications.
Equation [\ref{Aff}] can be interpreted as follows. \(\mathbf{A_{ff}}(\mathbf{r},\omega)\) can be expressed as the product of a spherical wave \(\left(\frac{\mu\,e^{\mathrm{i} k r}}{4\pi r}\right)\) and a directional weighting function \(\left(\mathbf{T}(\theta,\phi)=\int_{V'}\mathbf{J}\left(\mathbf{r'},\omega\right) e^{-\mathrm{i} k\, \mathbf{r'}.\,\mathbf{e}_r}dV'\right)\). Note that the dependency of \(\mathbf{T}\) on \(\theta\) and \(\phi\) originates from the dependency of \(\mathbf{e}_r\) to \(\theta\) and \(\phi\) (actually \(\mathbf{e}_r(\theta,\phi)\)). We actually expected this result.
Because as the waves leave the radiating source, they approach the spherical form regardless of the shape of the radiator. However, the shape of the radiator determines the strength of the spherical wave in each direction in space which is embedded in the weighting function \(\mathbf{T}(\theta,\phi)\).
Considering the above decomposition, one can obtain \(\mathbf{H}(\mathbf{r},\omega)\) as shown below. \begin{eqnarray} \mathbf{H}\left(\mathbf{r},\omega\right)&=&\frac{1}{\mu} \nabla\times\mathbf{A_{ff}}\left(\mathbf{r},\omega\right)=\frac{1}{\mu} \nabla\times\left(\frac{\mu\,e^{\mathrm{i} k r}}{4\pi r}\mathbf{T}(\theta,\phi)\right)\tag{7}\label{HA}\\&=&\frac{1}{4\pi}\left[ \nabla\left(\frac{e^{\mathrm{i} k r}}{r}\right)\times \mathbf{T}(\theta,\phi)+\frac{e^{\mathrm{i} k r}}{r}\,\nabla\times\mathbf{T}(\theta,\phi)\right]\nonumber\\&=&\frac{e^{\mathrm{i} k r}}{4\pi r}\left[\left(\mathrm{i}k-\frac{1}{r}\right)\mathbf{e}_r\times \mathbf{T}(\theta,\phi)\right.\nonumber\\&&\quad\quad +\frac{1}{r\sin(\theta)}\left(\frac{\partial}{\partial\theta}\left(T_\phi(\theta,\phi)\sin(\theta)\right)-\frac{\partial}{\partial \phi}T_\theta(\theta,\phi)\right)\mathbf{e}_r\nonumber\\&&\quad\quad+\left. \frac{1}{r\sin(\theta)}\frac{\partial}{\partial \phi}T_r(\theta,\phi)\mathbf{e}_\theta-\frac{1}{r}\frac{\partial}{\partial \theta}T_r(\theta,\phi)\mathbf{e}_\phi\right]\nonumber \end{eqnarray} which is a little bit complicated. However, as far as \(k\gg\frac{1}{r}\) (or equivalently \(r\gg\lambda\)), the above equation can be approximated as below. \begin{eqnarray} \mathbf{H}\left(\mathbf{r},\omega\right)&\simeq &\frac{e^{\mathrm{i} k r}}{4\pi r}\,\mathrm{i}k\mathbf{e}_r\times \mathbf{T}(\theta,\phi)\nonumber\\&=&\frac{1}{\mu}\mathrm{i}k\mathbf{e}_r\times\mathbf{A_{ff}}\left(\mathbf{r},\omega\right)\tag{8}\label{HAff} \end{eqnarray}
If you compare equation [\ref{HAff}] with equation [\ref{HA}], it seems that what we have done is just the substitution of \(\nabla\) with \(\mathrm{i}k\mathbf{e}_r\). Actually, it can be shown that when \(r\gg\lambda\), all field quantities can be approximated by using this substitution (you can check it for \(\mathbf{E}\left(\mathbf{r},\omega\right)\)).
Using this substitution, one can approximate \(\mathbf{E}\left(\mathbf{r},\omega\right)\) for \(r\gg\lambda\) as below. \begin{eqnarray} \mathbf{E}\left(\mathbf{r},\omega\right)&=& \mathrm{i} \omega\mathbf{A_{ff}}\left(\mathbf{r},\omega\right)-\frac{\nabla\big(\nabla\cdot\mathbf{A_{ff}}\left(\mathbf{r},\omega\right)\big)}{\mathrm{i}\omega\mu\,\varepsilon}\nonumber\\&\simeq &\mathrm{i}\omega\mathbf{A_{ff}}\left(\mathbf{r},\omega\right)-\frac{\mathrm{i}k\mathbf{e}_r\big(\mathrm{i}k\mathbf{e}_r\cdot\mathbf{A_{ff}}\left(\mathbf{r},\omega\right)\big)}{\mathrm{i}\omega\mu\,\varepsilon}\nonumber\\&=&\mathrm{i}\omega\mathbf{A_{ff}}\left(\mathbf{r},\omega\right)-\mathrm{i}\omega\mathbf{e}_r\left(\mathbf{e}_r\,.\,\mathbf{A_{ff}}\left(\mathbf{r},\omega\right)\right)\nonumber\\&=&\mathrm{i}\omega\left(A^\theta_\text{ff}\left(\mathbf{r},\omega\right)\mathbf{e}_\theta+A^\phi_\text{ff}\left(\mathbf{r},\omega\right)\mathbf{e}_\phi\right)\nonumber\\&=&\mathrm{i}\omega\mathbf{A^t_{ff}}\left(\mathbf{r},\omega\right)\tag{9} \end{eqnarray} where by \(\mathbf{A^t_{ff}}\left(\mathbf{r},\omega\right)\) we mean the transverse component of \(\mathbf{A_{ff}}\left(\mathbf{r},\omega\right)\).
Let us now summarize what we have done so far.
Firstly, we approximated the vector potential for far zone \(\frac{2L^2}{\lambda} < r\): \begin{equation} \mathbf{A_{ff}}(\mathbf{r},\omega)=\frac{\mu\,e^{\mathrm{i} k r}}{4\pi r}\int_{V'}\mathbf{J}\left(\mathbf{r'},\omega\right) e^{-\mathrm{i} k\, \mathbf{r'}.\,\mathbf{e}_r}dV'\tag{10}\label{Af} \end{equation}
Secondly, we approximated the fields for \(r\gg\lambda\): \begin{equation} \mathbf{H_{ff}}\left(\mathbf{r},\omega\right)=\frac{1}{\mu}\mathrm{i}k\mathbf{e}_r\times\mathbf{A_{ff}}\left(\mathbf{r},\omega\right)\tag{11}\label{Hf} \end{equation} \begin{equation} \mathbf{E_{ff}}\left(\mathbf{r},\omega\right)=\mathrm{i}\omega\mathbf{A^t_{ff}}\left(\mathbf{r},\omega\right)\tag{12}\label{Ef} \end{equation} These three equations (equation [\ref{Af}], [\ref{Hf}], and [\ref{Ef}]) govern the far zone of an arbitrary antenna. From now on, we consider everything at far zone unless explicitly stated. Therefore, we neglect the prefix "far field" and subscript "ff" for field quantities; for example instead of far field vector potential, we simply say vector potential and write \(\mathbf{A}\left(\mathbf{r},\omega\right)\).
Now we have every thing at hand. Therefore, let us calculate the vector potential for the dipole given in this problem by substituting the current distribution in equation [\ref{Af}]. \begin{eqnarray} \Rightarrow\mathbf{A}(\mathbf{r},\omega)&=&\frac{\mu\,e^{\mathrm{i} k r}}{4\pi r}\int_{-\frac{l}{2}}^{\frac{l}{2}}\int_{0}^{\infty}\int_{0}^{2\pi}\left[I_0 \, \sin\left(k(\frac{l}{2}-|z'|)\right) \,\frac{\delta(\rho')}{2\pi\rho'}\, \mathbf{e}_z\right] e^{-\mathrm{i} k\, \mathbf{r'}.\,\mathbf{e}_r} \rho' d\phi' d\rho' dz'\nonumber\\&=& \frac{\mu\,e^{\mathrm{i} k r}}{4\pi r}\int_{-\frac{l}{2}}^{\frac{l}{2}}\left[I_0 \, \sin\left(k(\frac{l}{2}-|z'|)\right)\, \mathbf{e}_z\right] e^{-\mathrm{i} k\,z'\cos(\theta)} dz'\nonumber \end{eqnarray}
It is easy but lengthy to calculate the integral. Below we calculate it step by step. First we expand the exponential into sin and cos functions. The integral over the imaginary part is zero since the function is odd. Thus, only the cos function remains. \begin{eqnarray} \Rightarrow\mathbf{A}(\mathbf{r},\omega)&=&\frac{\mu\,e^{\mathrm{i} k r}}{4\pi r}I_0\,\mathbf{e}_z\int_{-\frac{l}{2}}^{\frac{l}{2}}\sin\left(k(\frac{l}{2}-|z'|)\right)\big[\cos\left(\mathrm{i} k\,z'\cos(\theta)\right)-\mathrm{i}\sin\left(\mathrm{i} k\,z'\cos(\theta)\right)\big] dz'\nonumber\\&=&2\frac{\mu\,e^{\mathrm{i} k r}}{4\pi r}I_0\,\mathbf{e}_z\int_{0}^{\frac{l}{2}}\sin\left(k(\frac{l}{2}-z')\right)\cos\left(\mathrm{i} k\,z'\cos(\theta)\right) dz'\nonumber \end{eqnarray} Then we use "\(\sin(x)\cos(y)=\frac{1}{2}\left[\sin(x+y)+sin(x-y)\right]\)" to calculate the integral. \begin{eqnarray} \Rightarrow\mathbf{A}(\mathbf{r},\omega)&=&\frac{\mu\,e^{\mathrm{i} k r}}{4\pi r}I_0\,\mathbf{e}_z\int_{0}^{\frac{l}{2}}\left[\sin\left(k(\frac{l}{2}-z'+z'\cos(\theta))\right)+\sin\left(k(\frac{l}{2}-z'-z'\cos(\theta))\right) dz'\right]\nonumber\\&=&\frac{\mu\,e^{\mathrm{i} k r}}{4\pi r}I_0\,\mathbf{e}_z \left[\frac{\cos(k\frac{l}{2}\cos(\theta))-\cos(k\frac{l}{2})}{k(1-\cos(\theta))}+\frac{\cos(k\frac{l}{2}\cos(\theta))-\cos(k\frac{l}{2})}{k(1+\cos(\theta))}\right]\nonumber\\&=&\frac{\mu I_0}{2\pi}\frac{e^{\mathrm{i} k r}}{r}\,\frac{\cos(k\frac{l}{2}\cos(\theta))-\cos(k\frac{l}{2})}{k\sin^2(\theta)}\,\mathbf{e}_z\tag{13} \end{eqnarray}
Now, we can calculate \(\mathbf{H}(\mathbf{r},\omega)\) and \(\mathbf{E}(\mathbf{r},\omega)\) using equation [\ref{Hf}] and [\ref{Ef}]. \begin{equation} \Rightarrow\mathbf{H}(\mathbf{r},\omega)=\frac{-\mathrm{i} I_0}{2\pi}\frac{e^{\mathrm{i} k r}}{r}\,\frac{\cos(k\frac{l}{2}\cos(\theta))-\cos(k\frac{l}{2})}{\sin(\theta)}\,\mathbf{e}_\phi\tag{14}\label{Hl} \end{equation} \begin{equation} \Rightarrow\mathbf{E}(\mathbf{r},\omega)=\frac{-\mathrm{i} I_0}{2\pi}\sqrt{\frac{\mu}{\varepsilon}}\frac{e^{\mathrm{i} k r}}{r}\,\frac{\cos(k\frac{l}{2}\cos(\theta))-\cos(k\frac{l}{2})}{\sin(\theta)}\,\mathbf{e}_\theta\tag{15}\label{El} \end{equation} As can be seen, in far zone the fields are tangential and locally resemble plane waves.
2. Calculation of the Radiation Resistance - Small Dipole
One special case is when the length of the dipole antennas is much smaller that the wavelength (\(l\ll \lambda\)). Under this condition the current distribution on the antennas can be approximated as below. \[ \mathbf{J}\left(\mathbf{r},\omega\right) = \left\{ \begin{array}{l l} I_0\left(k(\frac{l}{2}-|z|)\right) \,\frac{\delta(\rho)}{2\pi\rho}\, \mathbf{e}_z & \quad |z| < \frac{l}{2}\\ 0 & \quad |z|\geq\frac{l}{2} \end{array} \right.\] where we approximated \(\sin(x)\) by \(x\). As can be seen, the current attains its maximum value at the center of the antenna and linearly decrease to zero as it approaches the edges. That is why this current distribution is called "triangular". This is a very good approximation for current distribution on short dipoles.
To calculate the radiated electric and magnetic fields in this case, one can again use equation [\ref{Af}] to find \(\mathbf{A}\left(\mathbf{r},\omega\right)\), and then equation [\ref{Hf}] and [\ref{Ef}] to find \(\mathbf{H}\left(\mathbf{r},\omega\right)\) and \(\mathbf{E}\left(\mathbf{r},\omega\right)\). Instead, we can just approximate equation [\ref{Hl}] and [\ref{El}] using \(\cos(x)\simeq1-\frac{x^2}{2}\). \begin{eqnarray} \Rightarrow\mathbf{H}(\mathbf{r},\omega)&=&\frac{-\mathrm{i} I_0}{2\pi}\frac{e^{\mathrm{i} k r}}{r}\,\frac{1-\frac{\left(k\frac{l}{2}\cos(\theta)\right)^2}{2}-1+\frac{\left(k\frac{l}{2}\right)^2}{2}}{\sin(\theta)}\,\mathbf{e}_\phi\nonumber\\&=&\frac{-\mathrm{i} k I_{tot}}{4\pi}\frac{e^{\mathrm{i} k r}}{r}\, \sin(\theta)\,\mathbf{e}_\phi\tag{16}\label{Htra} \end{eqnarray} \begin{eqnarray} \Rightarrow\mathbf{E}(\mathbf{r},\omega)&=&\frac{-\mathrm{i} I_0}{2\pi}\sqrt{\frac{\mu}{\varepsilon}}\frac{e^{\mathrm{i} k r}}{r}\,\frac{1-\frac{\left(k\frac{l}{2}\cos(\theta)\right)^2}{2}-1+\frac{\left(k\frac{l}{2}\right)^2}{2}}{\sin(\theta)}\,\mathbf{e}_\theta\nonumber\\&=&\frac{-\mathrm{i} k I_{tot}}{4\pi}\sqrt{\frac{\mu}{\varepsilon}}\frac{e^{\mathrm{i} k r}}{r}\, \sin(\theta)\,\mathbf{e}_\theta\tag{17}\label{Etra} \end{eqnarray} where, \[I_{tot}=\int_\frac{-l}{2}^\frac{l}{2}I_0\left(k(\frac{l}{2}-|z'|)\right)dz'=I_0 k \frac{l^2}{4}\]
By comparing these fields to those of an infinitesimal antenna (see again "The Infinitesimal Dipole"), it can be seen that they are the same except that the amplitude of the fields is different which is obviously due to different sizes of antennas.
Now let us calculate the radiation resistance of this antenna. The radiation resistance of an antennas is a resistance which can dissipate the same amount of power as the antenna radiate, if it is connected to the same source. In other words, if we neglect the ohmic loss in an antenna, the radiation resistance is exactly the real part of the input impedance of the antenna. The input impedance of an antenna is very important since it should match the input impedance of the transmitter (or receiver) in order to maximize the power transfer. It is not always easy to calculate the imaginary part of the input impedance since it depends of the near field behavior of the antenna.
However, the real part (radiation resistance) is easy to calculate, since it is connected to the radiated power which can be calculated using far fields. The radiation resistance is related to the transmitted power as follows, \begin{equation} P_r=\frac{1}{2} I_0^2 R_a\tag{18}\label{Ra} \end{equation} where, the left hand side is the total radiated power by antenna, and the right hand side is the average power dissipated by a resistor when it is connected to an alternating current source with an amplitude of \(I_0\) (which is also equal to the feeding current of the antenna).
Therefore, we first calculate the Poynting vector using far fields given in equation [\ref{Etra}] and [\ref{Htra}]. \begin{eqnarray} \mathbf{S}\left(\mathbf{r},\omega\right)&=&\frac{1}{2}\,\text{Real}\Big\{\mathbf{E}\left(\mathbf{r},\omega\right)\times \mathbf{H^*}\left(\mathbf{r},\omega\right)\Big\} \nonumber\\&=&\frac{ \mu^\frac{5}{2} \varepsilon^\frac{3}{2}I_0^2\omega^4 l^4}{512 \pi ^2}\frac{1}{r^2}\,sin^2(\theta)\mathbf{e}_r\tag{19}\label{Sff} \end{eqnarray} Then we calculate the radiated power by integrating the Poynting vector over the solid angle of a sphere. \begin{eqnarray} P_r&=&\int_0^{2\pi}\int_0^\pi\mathbf{S}\left(\mathbf{r},\omega\right)\,.\,\mathbf{e}_r\,r^2\sin(\theta)d\theta d\phi\nonumber\\&=&\frac{ \mu^\frac{5}{2} \varepsilon^\frac{3}{2}I_0^2\omega^4 l^4}{256 \pi}\int_0^\pi\sin^3(\theta)d\theta\nonumber\\&=&\frac{ \mu^\frac{5}{2} \varepsilon^\frac{3}{2}I_0^2\omega^4 l^4}{192 \pi}\tag{20}\label{Pr} \end{eqnarray} Now using equation [\ref{Ra}], radiation resistance can be obtained. \begin{equation} R_r=\frac{2P_r}{I_0^2}=\frac{ \mu^\frac{5}{2} \varepsilon^\frac{3}{2}\omega^4 l^4}{96 \pi} \tag{21} \end{equation} Note that this formula is valid as far as \(l\ll \lambda\).
As an example, the radiation resistance for a simple radio antenna with length of \(30^\text{cm}\), working at \(100^\text{MHz}\), and placed in air (\(\Rightarrow l=\frac{\lambda}{10}\ll\lambda\)) is approximately \(195^{m\Omega}\), which is extremely small. This resistance it much smaller than the \(50^\Omega\) output impedance of standard transmitters (or input impedance of standard receivers), and as a result a matching network is needed to convert \(195^{m\Omega}\) to \(50^{\Omega}\), which of course adds some complexity to our telecommunication system. That is why short dipoles are not good radiators. One way to increase the radiation resistance is to increase the length of the dipole. That is one reason why half-wave dipoles are more popular that short dipoles.
3. Important Special Cases: small dipole-, half-wavelength- and larger antennas
In this section we would like to see what will happen to the radiation pattern of a dipole antenna as its length is increased. To do so, we consider four dipoles with different lengths.
Using equation [\ref{El}] and [\ref{Hl}], one can calculate the Poynting vector for a general dipole as below.
\[\begin{eqnarray} \mathbf{S}\left(\mathbf{r},\omega\right)&=&\frac{1}{2}\,\text{Real}\Big\{\mathbf{E}\left(\mathbf{r},\omega\right)\times \mathbf{H^*}\left(\mathbf{r},\omega\right)\Big\} \nonumber\\&=&\frac{I^2_0}{4\pi^2}\sqrt{\frac{\mu}{\varepsilon}}\frac{1}{r^2}\,\frac{\left[\cos(k\frac{l}{2}\cos(\theta))-\cos(k\frac{l}{2})\right]^2}{\sin^2(\theta)}\,\mathbf{e}_r\tag{22}\label{Sl} \end{eqnarray}\]
For each case we just need to substitute the length of the antenna in equation [\ref{Sl}]. Therefore we obtain:
\[\begin{equation*} \mathbf{S}\left(\mathbf{r},\omega\right) =\mathbf{e}_r \, \frac{I^2_0}{4\pi^2}\sqrt{\frac{\mu}{\varepsilon}}\frac{1}{r^2}\,\left\{ \begin{matrix} \frac{\cos^2(\frac{\pi}{2}\cos(\theta))}{\sin^2(\theta)}\quad\quad\quad\quad &,(l=\frac{\lambda}{2})\\ \frac{\left[\cos(\pi\cos(\theta))+1\right]^2}{\sin^2(\theta)}\quad\quad &,(l=\lambda)\\ \frac{\left[\cos(1.4 \pi\cos(\theta))-\cos(1.4\pi)\right]^2}{\sin^2(\theta)}\quad\quad &, (l=1.4 \lambda)\\ \frac{\cos^2(\frac{3\pi}{2}\cos(\theta))}{\sin^2(\theta)}\quad\quad &, (l=1.5\lambda) \end{matrix} \right. \end{equation*}\]
As can be seen it is a little bit difficult to plot the radiation pattern by hand (which is almost always the case). However, there are simple ways to approximately sketch the radiation patterns to get a feeling about them. First of all, note that the radiation pattern is rotationally symmetric about the z-axis (\(\phi\)-independent). Secondly, find the directions in which the radiation pattern is zero (nulls of the antenna). Thirdly, between two consecutive nulls there is a local radiation maximum (which is called a lobe). Fourth, find the maximum direction of radiation, and plot approximately the radiation pattern in principal planes.
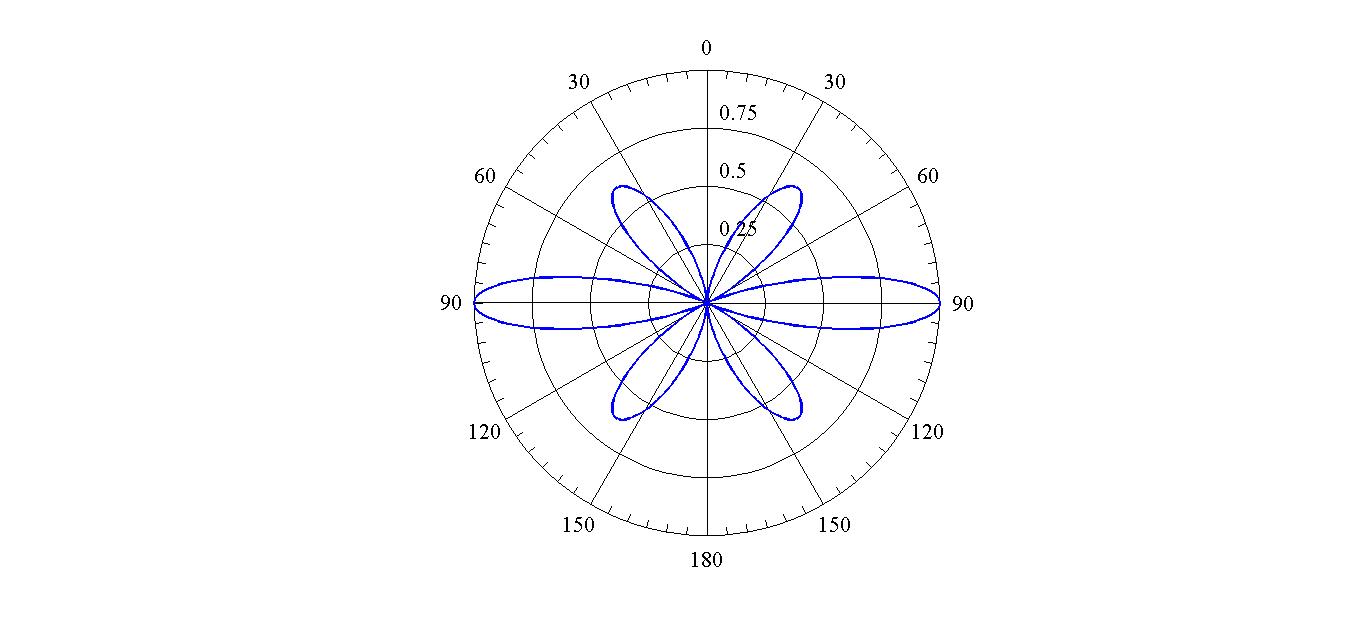
As an example, we do this procedure for the third dipole antenna \(l=1.4\lambda\) as below. \begin{equation} S_r^n\left(\mathbf{r},\omega\right)=\frac{\left[\cos(1.4 \pi\cos(\theta))-\cos(1.4\pi)\right]^2}{\sin^2(\theta)}\quad\quad,(l=1.4\lambda) \tag{23}\label{S1.4} \end{equation} Here, \(S_r^n\left(\mathbf{r},\omega\right)\) means the normalized radial component of the Poynting vector.
The nulls of the radiation pattern can be easily found. \[S_r^n\left(\mathbf{r},\omega\right)=0\rightarrow\cos(1.4 \pi\cos(\theta))-\cos(1.4\pi)=0\] \[\rightarrow \theta=\arccos \{1,-1+\frac{2}{1.4},1-\frac{2}{1.4},-1\}\] \[\Rightarrow Nulls:\quad \theta_\text{n}\simeq\{0,64.6^\circ,115.4^\circ,180^\circ\}\] From the above information it can be inferred that the radiation pattern has three lobes: one in \((0,64.6^\circ)\), one in \((64.6^\circ ,115.4^\circ)\), and the last one in \((115.4^\circ ,180^\circ)\). The radiation maxima are also located approximately between the nulls, i.e. at \(\theta_m\simeq\{32.3^\circ ,90^\circ ,147.7^\circ\}\).
Now we need to determine the principal planes. By substituting the values of \(\theta_m\) in equation [\ref{S1.4}], it appears that the maximum radiation occurs at \(\theta =90^\circ\). Since the antenna is omni-directional we are free to choose \(\phi\) for the direction of maximum radiation. Therefore, we choose \(\mathbf{e}_r(\theta=90^\circ,\phi=0)\) as the maximum direction of radiation. From equation [\ref{El}] we also know the electric field is directed along \(\mathbf{e}_\theta(\theta=\pi,\phi=0)=-\mathbf{e}_z\). Therefore the principal E-plane is x-z plane. In a similar way the principal H-plane can be determined as x-y plane.
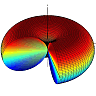
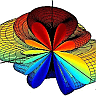
Considering all of the above facts, the radiation pattern for dipole antenna with \(l=1.4\lambda\) can be sketched as shown in Fig. 1 and 2.
The radiation in three dimensions is also shown in Fig. 3 below.
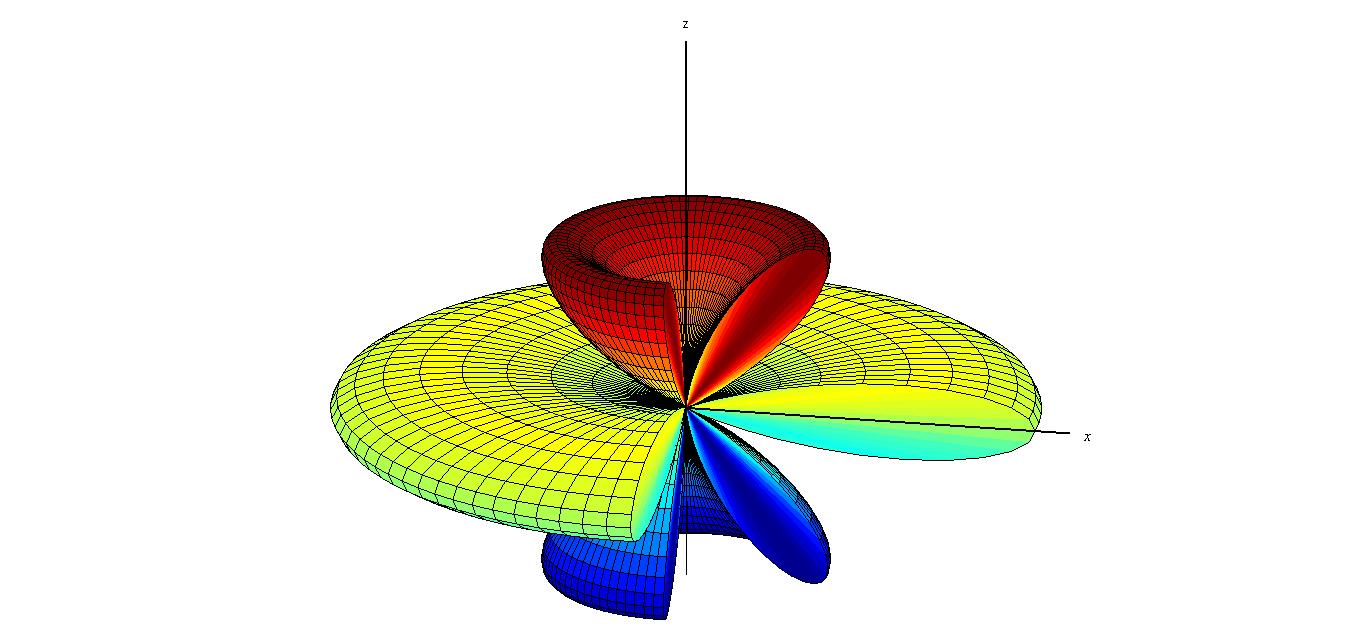
Using a computer program such as Mathematica or MATLAB, one can easily plot the exact radiation pattern. The radiation patterns for all other dipoles are plotted in Fig. 4 (due to rotational symmetry, the patterns are plotted only in E-plane).
Note that each pattern is normalized to its own maximum. For comparison the radiation pattern of an infinitesimal dipole is also plotted.
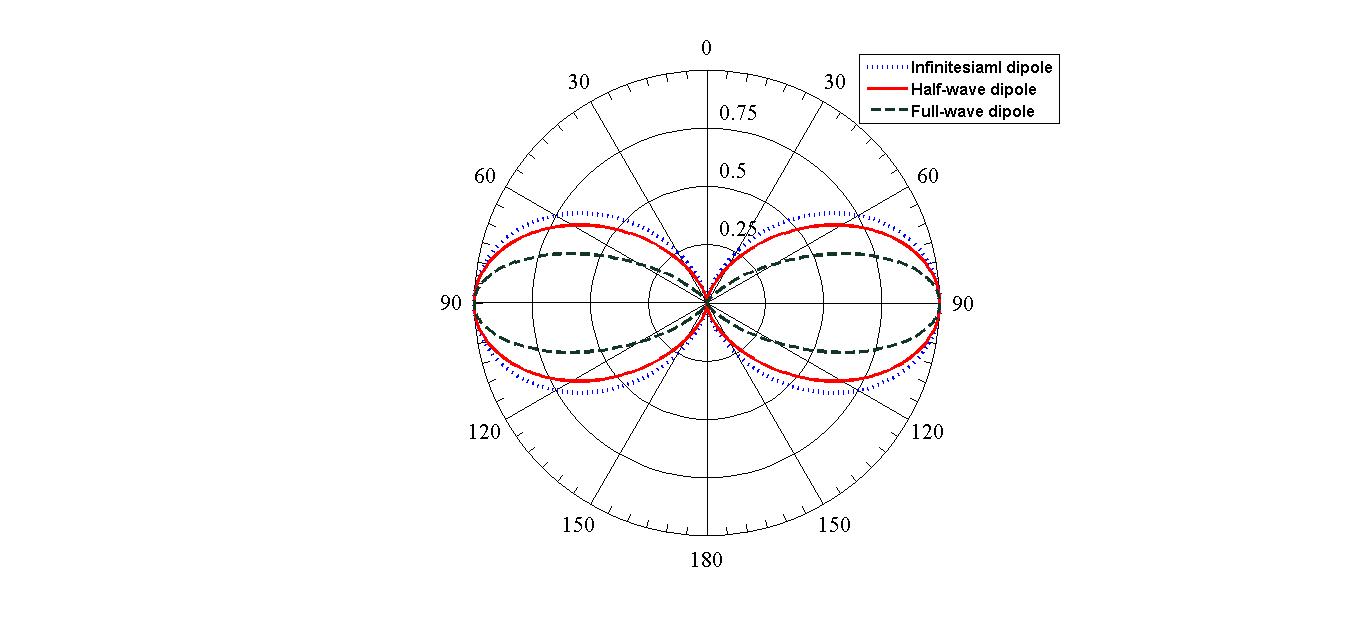
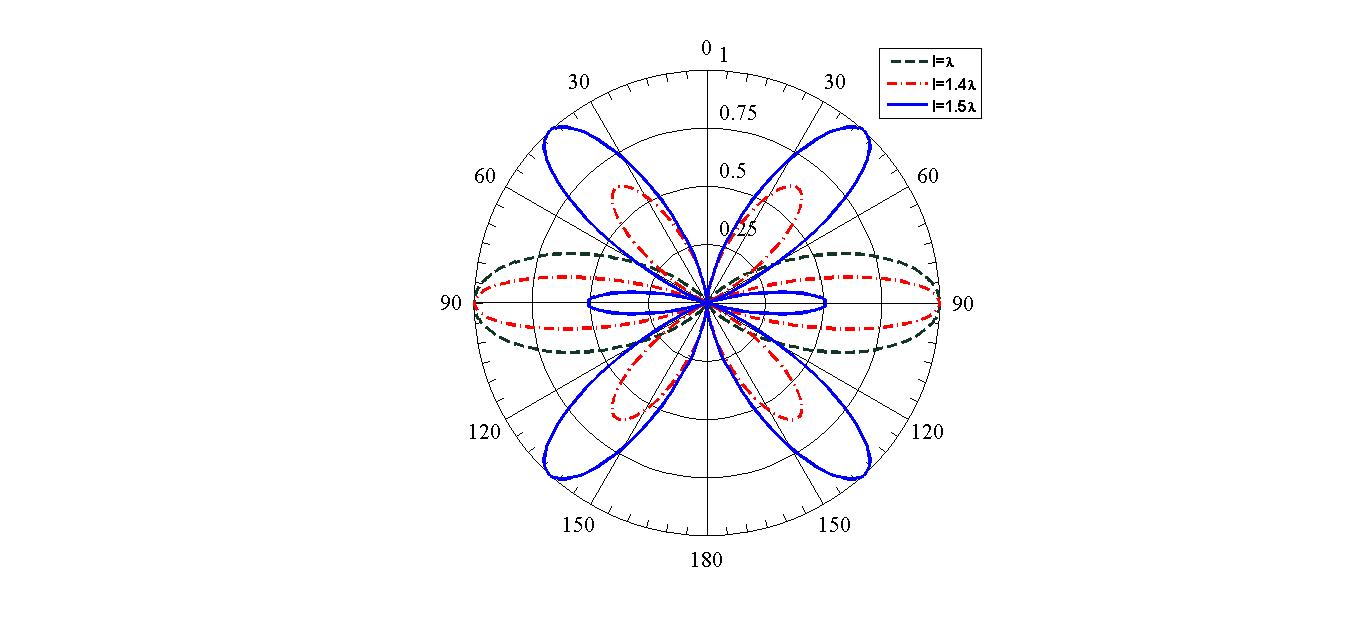
As can be seen, by increasing the length of the antenna the main lobe of the radiation pattern gets narrower and as a result directivity increases. However, as the length of the dipole becomes larger than the wavelength, two side lobes are added to the radiation pattern (as can be seen in figure (1) for \(l=1.4 \lambda\)).
As the length of the dipole is increased further, the side lobes become stronger (see Fig. 4 and compare the patterns for \(l=1.4 \lambda\) and \(l=1.5 \lambda\)). These side lobes decrease the directivity of the dipole.
That was quite a bit of work, wasn't it?!
In essence the far field of the finite dipole antenna is influenced by the separation of the charges. For some special cases we have seen how much.
We strongly encourage you to implement some of the formulas yourself and verify our radiation pattern! You will learn a lot about antenna theory by adapting the graphs and incorporating the mathematical formulas.