What happens if we take a wire, drill a hole in it and set some current in motion? Will we encounter a magnetic field?
Problem Statement
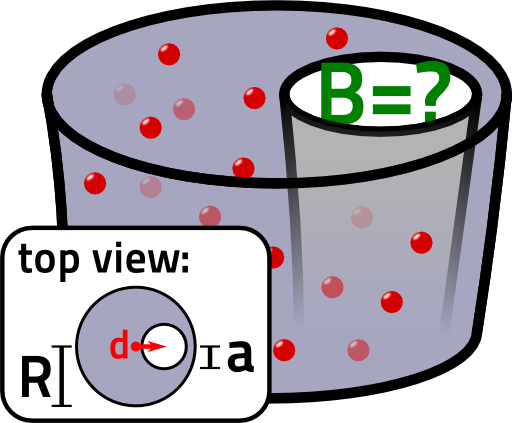A wire with radius \(R\) shall carry a constant current density \(j_{0}\). Inside the wire, there is further a hole with radius \(a<R\) which is displaced in \(x\) direction relative to the center of the with a certain distance \(d\). So, the current density may be described by
\[\begin{eqnarray*} \mathbf{j}\left(\mathbf{r}\right)&=&\begin{cases}j_{0} & \text{inside the wire}\\0 & \text{in the hole and outside}\end{cases} \end{eqnarray*}\]
and the hole by
\[\left\{ \mathbf{r}:\ \sqrt{\left(x-d\right)^{2}+y^{2}}\leq a\right\}\ . \]
Find the magnetic field inside of the hole.
You may regard our result from the problem "Magnetic Field of an Infinite Wire" as given.
Hints
Use the superposition principle to re-express the current in a more suitable way.
The azimuthal unit vector in cylindrical coordinates is related to cartesian coordinates by
\[\mathbf{e}_{\varphi} = -\frac{y}{\sqrt{x^{2}+y^{2}}}\mathbf{e}_{x}+\frac{x}{\sqrt{x^{2}+y^{2}}}\mathbf{e}_{y}\ .\]
If you understood the superposition principle, this worksheet should be pretty straight forward for you! Well ok, there's still some math to be done. Let's jump into the solution for the magnetic field of a hollow wire!
Solution
There are two different approaches to calculate the solution for this problem: The hard and the easy way. The hard way would be to write down integral equations following Ampère's law and do the math. But let's take a different route here!
We know that the solution inside of a cable with homogeneous current distribution is given by
\[\mathbf{B}\left(\mathbf{r}\right) = \frac{\mu_{0}j_{0}}{2}\rho\mathbf{e}_{\varphi}\text{ for }\rho\leq R.\]
Due to the principle of superposition, we may simply construct the current inside the cylinder as
\[\begin{eqnarray*} \mathbf{j}\left(\mathbf{r}\right)&\equiv&\mathbf{j}_{+}\left(\mathbf{r}\right)+\mathbf{j}_{-}\left(\mathbf{r}\right)\\&=&\begin{cases}j_{0}\left(1-\Theta\left(a-\sqrt{\left(x-d\right)^{2}+y^{2}}\right)\right) & \rho\leq R\\
0 & \rho>R\end{cases}\ . \end{eqnarray*}\]
Here, the \(\Theta\) relates to the Heaviside theta funktion which is one if its argument is greater than zero and zero if its less. We can say that the overall magnetic field is made up of two contributions:
\[\begin{eqnarray*} \mathbf{B}\left(\mathbf{r}\right)&=&\mathbf{B}_{+}\left(\mathbf{r}\right)+\mathbf{B}_{-}\left(\mathbf{r}\right)\\&=&\frac{\mu_{0}j_{0}}{2}\rho\mathbf{e}_{\varphi}-\frac{\mu_{0}j_{0}}{2}\rho^{\prime}\mathbf{e}_{\varphi}^{\prime}\Theta\left(a-\rho^{\prime}\right) \end{eqnarray*}\]
where we use the primed coordinates to denote the shift with respect to the \(x\) axis, e.g.
\[\begin{eqnarray*} \rho^{\prime}&=&\sqrt{x^{\prime2}+y^{\prime2}}=\sqrt{\left(x-d\right)^{2}+y^{2}}\text{ and}\\\mathbf{e}_{\varphi}^{\prime}&=&-\frac{y^{\prime}}{\sqrt{x^{\prime2}+y^{\prime2}}}\mathbf{e}_{x}^{\prime}+\frac{x^{\prime}}{\sqrt{x^{\prime2}+y^{\prime2}}}\mathbf{e}_{y}^{\prime}\\&=&-\frac{y}{\sqrt{\left(x-d\right)^{2}+y^{2}}}\mathbf{e}_{x}+\frac{x-d}{\sqrt{\left(x-d\right)^{2}+y^{2}}}\mathbf{e}_{y}\ . \end{eqnarray*}\]
Then we find
\[\begin{eqnarray*} \mathbf{B}\left(\mathbf{r}\right)&=&\frac{\mu_{0}j_{0}}{2}\sqrt{x^{2}+y^{2}}\left(-\frac{y}{\sqrt{x^{2}+y^{2}}}\mathbf{e}_{x}+\frac{x}{\sqrt{x^{2}+y^{2}}}\mathbf{e}_{y}\right)\\&&-\frac{\mu_{0}j_{0}}{2}\sqrt{\left(x-d\right)^{2}+y^{2}}\left(-\frac{y}{\sqrt{\left(x-d\right)^{2}+y^{2}}}\mathbf{e}_{x}+\frac{x-d}{\sqrt{\left(x-d\right)^{2}+y^{2}}}\mathbf{e}_{y}\right)\\&=&\frac{\mu_{0}j_{0}}{2}d\mathbf{e}_{y}\ . \end{eqnarray*}\]
Surprisingly, the field of a hollow wire with constant current is homogeneous. We also find that there is no magnetic field inside the hole if it is exactly at the center of the wire.
Furthermore, the field points perpendicular to the direction of the hole's displacement to the center of the wire, \(\mathbf{e}_{y}\perp d\mathbf{e}_{x}\). We may conclude from this that the field for a general displacement vector \(\mathbf{d}=d_{x}\mathbf{e}_{x}+d_{y}\mathbf{e}_{y}\) is given by
\[\mathbf{B}\left(\mathbf{r}\right) = \frac{\mu_{0}j_{0}}{2}\mathbf{e}_{z}\times\mathbf{d}\ .\]
In turn, a seemingly complicated problem was boiled down to a very basic statement. It is really interesting to see how the several geometrical parameters of the system influence the magnetic field of a hollow wire. Physics is quite surprising at times!