![]() If photons had a nonvanishing mass, the electromagnetic fields would show different characteristics than those we are used to: a wavelength dependence of the speed of light, modifications of Coulomb's and Ampères law and thus different fields for charges and dipoles and so on. Find out more about the photon mass and how related theories can be used to describe superconductivity.
If photons had a nonvanishing mass, the electromagnetic fields would show different characteristics than those we are used to: a wavelength dependence of the speed of light, modifications of Coulomb's and Ampères law and thus different fields for charges and dipoles and so on. Find out more about the photon mass and how related theories can be used to describe superconductivity.
Mathematical Description: The Proca Equations
In this first part we will loosely follow some lines of the very interesting review “The mass of the photon” by Tu et al., Reports on Progress in Physics 68 (2005) (PDF). More information about superconductivity can be found for example in Jackson's “Classical Electrodynamics” or Kittel's “Introduction to Solid State Physics” from an electrodynamics or solid states background, respectively.
The modifaction of Maxwells equations allowing massive photons was introduced by the romanian physicist Alexandru Proca in the early twentieth century and had a deep impact on particle physics. We will see in the second part that the mathematical framework Proca developed can also be used as a phenomenological description of superconductivity developped by the London brothers.
The so-called Proca-equations incorporate a photon mass \(m_{\gamma}\) into Maxwell's equations: Both Gauss's and Ampères law are modified (statics!):
For visibility, we may use the abbreviation \(\mu_{\gamma}=m_{\gamma}c/\hbar\).
Note that the latter equations can be derived from the Lagrangian density of the fields with an extra term
\[\propto\mu_{r}A_{\mu}\left(x^{\nu}\right)A^{\mu}\left(x^{\nu}\right)\]
in relativistic notation taking the static limit. In the Proca-equations, the potentials \(\phi\left(\mathbf{r}\right)\) and \(\mathbf{A}\left(\mathbf{r}\right)\).
Note that the potentials are defined / written explicitly and obtain a direct physical meaning which is otherwise not the case in classical electrodynamics.
Let us concentratete on the magnetic part and how the fields are changing due to the photon mass. Using \(\mathbf{B}\left(\mathbf{r}\right)=\nabla\times\mathbf{A}\left(\mathbf{r}\right)\), we find with
\[\nabla\times\nabla\times\mathbf{A}\left(\mathbf{r}\right)=\nabla\left(\nabla\cdot\mathbf{A}\left(\mathbf{r}\right)\right)-\Delta\mathbf{A}\left(\mathbf{r}\right)\]
in Coulomb gauge,
\[\nabla\cdot\mathbf{A}\left(\mathbf{r}\right)=0\ ,\]
\[\left(\Delta-\mu_{\gamma}^{2}\right)\mathbf{A}\left(\mathbf{r}\right) = -\mu_{0}\mathbf{j}\left(\mathbf{r}\right)\ .\]
This linear partial differential equation can be conveniently solved using the Green's function for which
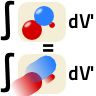
\[\mathbf{A}\left(\mathbf{r}\right) = \int G\left(\mathbf{r},\mathbf{r}^{\prime}\right)\mathbf{j}\left(\mathbf{r}^{\prime}\right)dV^{\prime}\ .\]
However, in contrast to the \(\propto1/\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\)-dependency in usual electro- and magnetostatics, we obtain
\[G\left(\mathbf{r},\mathbf{r}^{\prime}\right) = \frac{\mu_{0}}{4\pi}\frac{\exp\left(-\mu_{\gamma}\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|}\ .\]
This Green function with its exponential decay is characteristic for so-called Yukawa potentials. Now, for the magnetic dipole moment,
\[\mathbf{m} = \frac{1}{2}\int\mathbf{r}^{\prime}\times\mathbf{j}\left(\mathbf{r}^{\prime}\right)dV^{\prime}\ ,\]
we find the dipole field for the magnetic induction to be
\[\mathbf{B}_{\mathrm{D}}\left(\mathbf{r}\right) = \frac{\mu_{0}}{4\pi}\frac{e^{-\mu_{\gamma}r}}{r^{3}}\left\{ \left[1+\mu_{\gamma}r+\frac{1}{3}\mu_{\gamma}^{2}r^{2}\right]\left[3\left(\mathbf{m}\cdot\mathbf{e}_{r}\right)\mathbf{e}_{r}-\mathbf{m}\right]-\frac{2}{3}\mu_{\gamma}^{2}r^{2}\mathbf{m}\right\} \ .\]
This dipole field is thus modified with respect to the usual result without photon mass. The first term leads to a strengthening of the usual dipole,
\[\mathbf{m}\rightarrow\left[1+\mu_{\gamma}r+\frac{1}{3}\mu_{\gamma}^{2}r^{2}\right]\mathbf{m}\]
but we can also see the characteristic Yukawa fall-off in the pre-factor.
The second term, however, leads to a further contribution to the magnetic induction. Assuming that the magnetic field of the earth is basically a dipole, Schrödinger suggested that the ratio of the ordinary dipole moment to the second term in \(\mathrm{\mathbf{B}_{D}}\) should be measurable with respect to the usual modified first term.
In 1955, Bass and Schrödinger analysed magnetic survey data from 1922 and found an upper limit of \(m_{\gamma}\lesssim10^{-47}\,\)g.
A lot of studies followed employing different methods like large-scale observations of magnetic fields in the universe. All investigastions resulted in a maximum limit of the photon mass more or less close to the official value of the particle data group, \(m_{\gamma}\leq10^{-49}\,\)g. However, the question if the photon has a mass is still open and may never be solved conclusive; how could one ever find the photon mass to be exactly zero? Maybe you have the right idea - Stockholm is calling!
Magnetic Fields in Superconductors: The London Penetration Depth
Now, how can we use massive photons to phenomenologically describe superconductivity? The London theory of superconductors gives an explanation of the so-called Meissner effect. This effect, discovered in the thirties of the last century, states that a magnetic field can only have a finite penetration into a superconductor, which the Londons explained assuming that photons inside a superconductor acquire an effective mass. Of course, this explanation links the Proca form of the magnetic field to the Meissner effect. Let us understand the finite penetration depht of the magnetic fields into superconductors in the following.
We start with an expression for the current in a non-relativistic conductor given by
\[\mathbf{j}\left(\mathbf{r}\right) = \mathbf{j}_{\mathrm{cond}}\left(\mathbf{r}\right)+\mathbf{j}_{\mathrm{ext}}\left(\mathbf{r}\right)=qn_{q}\mathbf{v}\left(\mathbf{r}\right)+\mathbf{j}_{\mathrm{ext}}\left(\mathbf{r}\right)\ .\]
For the moment, let us not consider any external charges but only the conductive contribution inside the superconductor, hence \(\mathbf{j}_{\mathrm{ext}}\left(\mathbf{r}\right)=0\).
The generalized momentum of a charged particle in an electromagnetic field is given by \(\mathbf{p}=m_{q}\mathbf{v}+\frac{q}{c}\mathbf{A}\), so we might express the conductive current as
\[\mathbf{j}\left(\mathbf{r}\right) = \frac{qn_{q}}{m_{q}}\left(\mathbf{p}\left(\mathbf{r}\right)-\frac{q}{c}\mathbf{A}\left(\mathbf{r}\right)\right)\ .\]
Now the Londons assumed that the superconducting state is characterized by a vanishing generalized momentum, \(\mathbf{p}=0\). This assumption got its theoretical foundation later on quantum mechanical grounds and implies here
\[\mathbf{j}\left(\mathbf{r}\right) = -\frac{q^{2}n_{q}}{m_{q}c}\mathbf{A}\left(\mathbf{r}\right)\ .\]
Now inserting this current into Ampère's law, we obtain
\[\begin{eqnarray*} \nabla\times\mathbf{B}\left(\mathbf{r}\right)&=&\mu_{0}\mathbf{j}\left(\mathbf{r}\right)=-\mu_{0}\frac{q^{2}n_{q}}{m_{q}c}\mathbf{A}\left(\mathbf{r}\right)\ ,\\-\Delta\mathbf{A}\left(\mathbf{r}\right)&=&-\mu_{0}\frac{q^{2}n_{q}}{m_{q}c}\mathbf{A}\left(\mathbf{r}\right) \end{eqnarray*}\]
using \(\mathbf{B}\left(\mathbf{r}\right)=\nabla\times\mathbf{A}\left(\mathbf{r}\right)\) and \(\nabla\cdot\mathbf{A}\left(\mathbf{r}\right)=0\)
With the abbreviation
\[\mu_{\mathrm{L}}^{2} = \mu_{0}\frac{q^{2}n_{q}}{m_{q}c}\]
we find, reincorporating an external current,
\[\left(\Delta-\mu_{\mathrm{L}}^{2}\right)\mathbf{A}\left(\mathbf{r}\right) = -\mathbf{j}_{\mathrm{ext}}\left(\mathbf{r}\right)\ .\]
So, in the end, the conductive current we introduced can be interpreted as an effective photon mass and leads to an equivalent formulation as the one given by Proca. However, in the London theory, \(\mu_{\gamma}\) is replaced by \(\mu_{\mathrm{L}}\). Both \(\mu\)'s have the dimension of an inverse length and \(\lambda_{\mathrm{L}}=1/\mu_{\mathrm{L}}\) is termed the London penetraton depth.
For low-temperature superconductors, \(\mu_{\mathrm{L}}\) is in the order of a few µm.
Now we have everything at hand to understand why \(\lambda_{\mathrm{L}}\) is indeed the penetration depth of the magnetic field - We strongly encourage you to find out why solving "Superconductors and Their Magnetostatic Fields". In the work sheet you will also find the solution and hints.