The Infinitesimal Dipole - Radiation Pattern, Directivity and all that

In this problem we first investigate the radiation properties of a very short and thin filament of current. Although this filament of current as an antenna is not physically realizable, as a mathematical model it will help us to understand the general behavior of antennas. Here we also introduce some of the fundamental antenna parameters.

Problem Statement

A very thin and short antenna which works at frequency ω has the the following current distribution.

where J₀ is the amplitude of the current distribution, δ(r) is delta function, and $\hat{\mathbf{z}}$ is the unit vector in z direction of the Cartesian coordinate.

Assume that the current distribution is placed in a homogeneous environment with permitivity ε and permeability μ, respectively. Remember that this current distribution represents the infinitesimal antenna!

1. Find the  electric and magnetic fields E(r,ω) and H(r,ω) that are generated by the current.
2. Sketch the far field radiation pattern of the antenna in transverse and vertical planes (e.g. x-y and x-z planes).
3. Calculate the half power beamwidth (HW) of the antenna in x-z plane and its directivity.

Hints

1. First find vector potential A(r,ω) by solving the equation below.

The latter equation is kind of famous as it resembles the inhomogeneous wave equation in frequency space, i.e. the inhomogeneous Helmholtz equation.

Try to use the symmetries in the problem to simplify this equation. Then, find E(r,ω) and H(r,ω) using the following equations.

2. Approximate E(r,ω) and H(r,ω) for $r\gg \lambda$ to find far fields (e.g. ${\mathbf{E}}_{\mathbf{ff}}(\mathbf{r},\omega )$ and ${\mathbf{H}}_{\mathbf{ff}}(\mathbf{r},\omega )$). Then, using far fields calculate the Poynting vector. Finally, sketch the radial component of the Poynting vector versus $\phi$ (azimuth angle) in x-y plane, and versus $\theta$ (polar angle) in x-z plane.

3. Half power beamwidth (HW), in x-z plane, is defined as the width of the angular interval in which the radiation intensity is more than half of the maximum radiation intensity.

Directivity is defined as below.

$$D(\theta ,\phi )=\frac{\text{radiation intensity}}{\text{average of radiation intensity over all directions}}$$

Solving the infinitesimal dipole

Let's get dirty and figure out all the mathemics behind this radiation task!

1. The first step to solve this problem is to find the vector potential. Therefore, we start with the equation below.

$$\begin{array}{}\text{(1)}& {\mathrm{\nabla }}^2\mathbf{A}(\mathbf{r},\omega )+{\omega }^2\mu \epsilon \mathbf{A}(\mathbf{r},\omega )=-\mu J_0\delta (\mathbf{r})\hat{\mathbf{z}}\end{array}$$

We can split this equation into three equations, each in one direction of the Cartesian coordinate (e.g. $\hat{\mathbf{x}}\mathbf{,}\hat{\mathbf{y}}\mathbf{,}\mathbf{\text{and}}\hat{\mathbf{z}}$). If you do that, you will see that for $A_x(\mathbf{r},\omega )$ and $A_y(\mathbf{r},\omega )$ there is no source term (right hand side of the their governing equations is zero). Therefore, $A_x(\mathbf{r},\omega )$ and $A_y(\mathbf{r},\omega )$ are zero.

$$\begin{array}{}\text{(2)}& \Rightarrow \mathbf{A}(\mathbf{r},\omega )=A_z(\mathbf{r},\omega )\hat{\mathbf{z}}\end{array}$$

Using this fact, equation [$\text{1}$] can be simplified as below.

$$\begin{array}{}\text{(3)}& {\mathrm{\nabla }}^2{A}_z(\mathbf{r},\omega )+{\omega }^2\mu \epsilon A_z(\mathbf{r},\omega )=-\mu J_0\delta (\mathbf{r})\end{array}$$

Since the source term (right hand side of equation [$\text{3}$]) has a spherical symmetry (since it does not depend on $\theta$ and $\phi$), $A_z(\mathbf{r},\omega )$ is also spherically symmetric (there is not any preferred direction for $A_z(\mathbf{r},\omega )$ ).

Thus, $A_z(\mathbf{r},\omega )$ is only a function of radial distance from the source point, i.e. $A_z(\mathbf{r},\omega )=A_z(r,\omega )$. Due to this spherical symmetry we use spherical coordinates to expand equation [$\text{3}$] as shown below.

$$\begin{array}{}\text{(4)}& \frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial A_z(r,\omega )}{\partial r}\right)+{\omega }^2\mu \epsilon A_z(r,\omega )=-\mu J_0\delta (\mathbf{r})\end{array}$$

The right hand side of equation [$\text{4}$] is only non-zero in the center of coordinate. So, our strategy to tackle equation [$\text{4}$] is to solve it for all space excluding the center, and then satisfying the source condition at center (we will see the second part later). Therefore, we solve the following equation first.

$$\begin{array}{}\text{(5)}& \frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial A_z(r,\omega )}{\partial r}\right)+{\omega }^2\mu \epsilon A_z(r,\omega )=0,(r\ne 0)\end{array}$$

To make equation [$\text{5}$] a little bit simpler, without loss of generality we define $A_z(r,\omega )$ as below.

$$\begin{array}{}\text{(6)}& A_z(r,\omega )=\frac{\varphi (r,\omega )}{r}\end{array}$$

By substituting equation [$\text{6}$] in equation [$\text{5}$] we obtain

$$\frac{{\partial }^2\varphi (r,\omega )}{\partial r^2}+{\omega }^2\mu \epsilon \varphi (r,\omega )=0,(r\ne 0)$$

$$\Rightarrow \varphi (r,\omega )=C_1{e}^{ikr}+C_2{e}^{-ikr}$$

which results in,

$$A_z(r,\omega )=C_1\frac{e^{ikr}}{r}+C_2\frac{e^{-ikr}}{r}$$

where, $k=\omega \sqrt{\mu \epsilon }$, and $C_1$ and $C_2$ are two arbitrary constants.

Now, we need to determine $C_1$ and $C_2$. Firstly, as we have used $e^{-i\omega t}$ as the time dependency of harmonic fields (see Basics), $C_1{e}^{ikr}$ corresponds to an outgoing wave while $C_2{e}^{-ikr}$ is an incoming wave. Since we assumed that the antenna is in a homogeneous space, electromagnetic waves go away from the antenna. Therefore, there is not any incoming wave. So, $C_2$ is zero.

$$\begin{array}{}\text{(7)}& \Rightarrow A_z(r,\omega )=C_1\frac{e^{ikr}}{r}\end{array}$$

Note that equation [$\text{7}$] is valid for $r\ne 0$ and we need to determine $C_1$ in a way that equation [$\text{7}$] satisfies equation [$\text{3}$] at $r=0$ as well (source condition). This step is a little bit tricky. Since $r=0$ is a singular point of $A_z(r,\omega )$, it is not possible to discuss about the value of $A_z(r,\omega )$ exactly at $r=0$ and relate it to the source. However, $A_z(r,\omega )$ is integrable over a volume around $r=0$, let say a small sphere with radius $a$. Therefore, we can relate the integral value of $\mathbf{A}(\mathbf{r},\omega )$ to the integral value of source $(\mathbf{J}(\mathbf{r},\omega ))$ over this volume to determine $C_1$. To do that, we integrate both sides of the equation [$\text{3}$] over a very small sphere around $r=0$ with radius $a$ as it approaches zero. For every term in equation [$\text{3}$] we calculate the integral as shown below.

$$\begin{array}{rcl}{\int }_{v_a}{\mathrm{\nabla }}^2{A}_z(\mathbf{r},\omega )dv& =& {\int }_{v_a}\mathrm{\nabla }\cdot (\mathrm{\nabla }{A}_z(\mathbf{r},\omega ))dv\\ & =& {\int }_{s_a}\mathrm{\nabla }{A}_z(\mathbf{r},\omega ).d\mathbf{s}\\ & =& {\int }_{s_a}{C}_1{e}^{ikr}(\frac{ik}{r}-\frac{1}{r^2})r^2\sin (\theta )d\theta d\phi \\ & =& 4\pi C_1{e}^{ika}(ika-1)\end{array}$$

$$\begin{array}{}\text{(8)}& \Rightarrow \underset{a\to 0}{lim}{\int }_{v_a}{\mathrm{\nabla }}^2{A}_z(\mathbf{r},\omega )dv=-4\pi C_1\end{array}$$

$$\begin{array}{}\text{(9)}& \underset{a\to 0}{lim}{\int }_{v_a}{\omega }^2\mu \epsilon A_z(\mathbf{r},\omega )dv={\omega }^2\mu \epsilon \underset{a\to 0}{lim}{\int }_{v_a}{C}_1\frac{e^{ikr}}{r}{r}^2\sin (\theta )d\theta d\phi dr=0\end{array}$$

$$\begin{array}{}\text{(10)}& \underset{a\to 0}{lim}{\int }_{v_a}-\mu J_0\delta (\mathbf{r})dv=-\mu J_0\underset{a\to 0}{lim}{\int }_{v_a}\delta (\mathbf{r})dv=-\mu J_0\end{array}$$

By putting the results of equation [$\text{8}$], [$\text{9}$], and [$\text{10}$] together, $C_1$ can be found

$$C_1=\frac{\mu J_0}{4\pi }$$

and therefore,

$$A_z(r,\omega )=\frac{\mu J_0}{4\pi }\frac{e^{ikr}}{r}$$

$$\begin{array}{}\text{(11)}& \Rightarrow \mathbf{A}(\mathbf{r},\omega )=\frac{\mu {\mathbf{J}}_{\mathbf{0}}}{4\pi }\frac{e^{ikr}}{r}\end{array}$$

Now, one can calculate the magnetic field easily as follows.

$$\begin{array}{rcl}\mathbf{H}(\mathbf{r},\omega )& =& \frac{1}{\mu }\mathrm{\nabla }\times \mathbf{A}(\mathbf{r},\omega )\\ & =& \frac{1}{\mu }\mathrm{\nabla }\times \left(\frac{\mu J_0}{4\pi }\frac{e^{ikr}}{r}\hat{\mathbf{z}}\right)\\ & =& \frac{J_0}{4\pi }\mathrm{\nabla }\left(\frac{e^{ikr}}{r}\right)\times \hat{\mathbf{z}}\\ & =& \frac{J_0}{4\pi }{e}^{ikr}(\frac{ik}{r}-\frac{1}{r^2})\hat{\mathbf{r}}\times \hat{\mathbf{z}}\end{array}$$

$$\begin{array}{}\text{(12)}& \Rightarrow \mathbf{H}(\mathbf{r},\omega )=-\frac{ik{J}_0}{4\pi }\frac{e^{ikr}}{r}(1+\frac{i}{kr})\sin (\theta )\hat{\phi }\end{array}$$

to calculate the electric field, we do the following.

$$\begin{gathered} \begin{array}{rcl}\mathrm{\nabla }(\mathrm{\nabla }\cdot \mathbf{A}(\mathbf{r},\omega ))& =& \mathrm{\nabla }[\frac{\mu J_0}{4\pi }{e}^{ikr}(\frac{ik}{r}-\frac{1}{r^2})\hat{\mathbf{r}}\cdot \hat{\mathbf{z}}]\\ & =& \frac{\mu J_0}{4\pi }\mathrm{\nabla }[e^{ikr}(\frac{ik}{r}-\frac{1}{r^2}) \\ cos(\theta )]\\ & =& \frac{\mu J_0}{4\pi }{e}^{ikr}[ \\ cos(\theta )(-\frac{k^2}{r}-\frac{2ik}{r^2}+\frac{2}{r^3})\hat{\mathbf{r}}+\sin (\theta )(-\frac{ik}{r^2}+\frac{1}{r^3})\hat{\theta }]\end{array} \end{gathered}$$

$$\begin{gathered} \begin{array}{rcl}\Rightarrow \mathbf{E}(\mathbf{r},\omega )& =& i\omega \mathbf{A}(\mathbf{r},\omega )-\frac{\mathrm{\nabla }(\mathrm{\nabla }\cdot \mathbf{A}(\mathbf{r},\omega ))}{i\omega \mu \epsilon }\\ \text{(13)}& & =& \frac{i\omega \mu J_0}{4\pi }\frac{e^{ikr}}{r}[ \\ cos(\theta )(-\frac{2i}{kr}+\frac{2}{(kr{)}^2})\hat{\mathbf{r}}+\sin (\theta )(-1-\frac{i}{kr}+\frac{1}{(kr{)}^2})\hat{\theta }]\end{array} \end{gathered}$$

2. Lets first clarify what we mean by radiation pattern of an antenna. Generally, the radiation pattern is defined as the radiation intensity (radial component of the Poynting vector) as a function of direction in space ($\phi$ and $\theta$). Since in reality the receiver and transmitter antennas are located very far from each other, the calculation and measurement of radiation patterns are usually done using the fields in far distances form antennas. Hence, the fields are called far fields and the resultant pattern is called far filed radiation pattern or briefly far field pattern (we will see in Problem One how to precisely define the far field zone of an antenna). It should be noted that the radiation pattern is usually normalized to its maximum.
Based on what is mentioned, firstly, we need to calculate far fields. According to equation [$\text{12}$] and [$\text{13}$], for $kr\gg 1$, the electric and magnetic fields can be approximated as below.

$$\begin{array}{}\text{(14)}& {\mathbf{H}}_{\mathbf{ff}}(\mathbf{r},\omega )\cong \frac{-ik{J}_0}{4\pi }\frac{e^{ikr}}{r}\sin (\theta )\hat{\phi }\end{array}$$

$$\begin{array}{}\text{(15)}& {\mathbf{E}}_{\mathbf{ff}}(\mathbf{r},\omega )\cong \frac{-i\omega \mu J_0}{4\pi }\frac{e^{ikr}}{r}\sin (\theta )\hat{\theta }\end{array}$$

This approximation is only valid for fields at large distance form the antenna ($kr\gg 1$).This condition can also be rewritten in the following way.

$$\begin{array}{}\text{(16)}& kr\gg 1\Rightarrow r\gg \frac{1}{k}=\frac{1}{\omega \sqrt{(}\mu \epsilon )}=\frac{c}{\omega }=\frac{\lambda }{2\pi }\Rightarrow r\gg \lambda \end{array}$$

where $\lambda$ is the wavelength of the wave in the medium. As can be seen, far field zone for an infinitesimal antenna is all points of space for which the distance to the antenna is much larger than wavelength.

Now, the Poynting vector can be calculated as below.

$$\begin{array}{rcl}{\mathbf{S}}_{\mathbf{ff}}(\mathbf{r},\omega )& =& \frac{1}{2}\text{Real}\{{\mathbf{E}}_{\mathbf{ff}}(\mathbf{r},\omega )\times {\mathbf{H}}_{\mathbf{ff}}^{\mathbf{\ast }}(\mathbf{r},\omega )\}\\ \text{(17)}& & =& \frac{{\mu }^{\frac{3}{2}}{\epsilon }^{\frac{1}{2}}{\omega }^2{J}_0^2}{32{\pi }^2}\frac{1}{r^2}si{n}^2(\theta )\hat{\mathbf{r}}\end{array}$$

As can be seen the intensity drops as $\frac{1}{r^2}$ which is expected from the law of conservation of energy.
The far field radiation pattern can be calculated easily by normalizing equation [$\text{17}$].

$$\begin{array}{}\text{(18)}& S_{ff}^n\left(\theta \mathbf{,}\phi \right)=si{n}^2(\theta )\end{array}$$

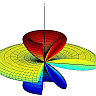
Here, the superscript 'n' denotes the normalization. The far filed radiation pattern is depicted in figure (1) in three dimensions.

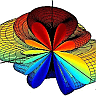
Conventionally, radiation patterns are drawn in some cut-planes (there are some standard planes which we will define in Problem One), since it is easier to see the details of the pattern which are not visible in a three dimensional figure. Here, due to rotational symmetry, it is sufficient to draw the pattern only in x-z plane. However, to show the rotational symmetry it is better to draw the pattern in x-y plane as well. The far field radiation pattern in x-y and x-z planes are shown in figure (2) and (3).

 

3. In this last step we just want to introduce some simple antenna parameters and the way to calculate them, such as half power beamwidth (HW) and "directivity". All of these parameters are calculated using the Poynting vector, therefore, they just provide different pictures of the radiation characteristics of the antenna.
HW, in a determined plane, is defined as the width of the angular interval in which the radiation intensity is more than half of the maximum radiation intensity.
According to equation [$\text{17}$], one can calculate the HW of the antenna in x-z plane as below.

$$\frac{{\mu }^{\frac{3}{2}}{\epsilon }^{\frac{1}{2}}{\omega }^2{J}_0^2}{32{\pi }^2}\frac{1}{r^2}si{n}^2(\theta )\frac{1}{2}\times \frac{{\mu }^{\frac{3}{2}}{\epsilon }^{\frac{1}{2}}{\omega }^2{J}_0^2}{32{\pi }^2}\frac{1}{r^2}$$

$$\Rightarrow si{n}^2(\theta )\frac{1}{2}\Rightarrow \theta \in (-{45}^{\circ },{45}^{\circ })$$

$$\Rightarrow HW={90}^{\circ }$$

This a measure which means that the antenna radiates effectively over 90 degree in the x-z plane which is a quite large angle. Although HW is an important parameter, it does not indicate in which directions the antenna has higher radiation. Therefore, we define "directivity" to address this question.
Since the radiated intensity of an antenna is a function of the direction of radiation, a criterion is needed to characterize and quantify this dependency. This criterion is the so-called "directivity function" and defined as below.

$$\begin{array}{}\text{(19)}& D(\theta ,\phi )=\frac{\text{radiation intensity}}{\text{average of radiation intensity over all directions}}\end{array}$$

Physically, this function describes the ability of an antenna to send power in a specific direction and compares it to the average power radiated in all directions.
Using equation [$\text{19}$], the directivity of our infinitesimal antenna can be obtained as below.

$$\begin{array}{rcl}D(\theta ,\phi )& =& \frac{S_{ff}^n\left(\theta \mathbf{,}\phi \right)}{\frac{1}{4\pi }{\int }_0^{2\pi }{\int }_0^{\pi }{S}_{ff}^n\left(\theta \mathbf{,}\phi \right)\sin (\theta )d\theta d\phi }\\ & =& \frac{si{n}^2(\theta )}{\frac{1}{4\pi }{\int }_0^{2\pi }{\int }_0^{\pi }si{n}^3(\theta )d\theta d\phi }\\ \text{(20)}& & =& \frac{3}{2}si{n}^2(\theta )\end{array}$$

For example the directivity of the antenna in the direction of $\theta ={60}^{\circ },\phi ={30}^{\circ }$ is equal to 1.125, which mean that the antenna radiates 1.125 times larger than the average radiation in this direction( note that the maximum directivity for an infinitesimal antenna is 1.5). As can be seen in equation [$\text{20}$], the diectivity is not a function of azimuth angle. Therefore, it is said that the antenna is omni-directional, which means that there is one plane in which the directitity is constant (here x-y plane).

Now this was a lot of insights for antenna theory! We strongly encourage you to do some more calculations on your own to get a feeling for the mathematics behind the infinitesimal dipole antenna!