Spherical Capacitor with Varying Permittivity

In general, capacitance calculations can be quite cumbersome involving complicated integrals. Whenever symmetries are present, we may find the capacitances much easier. Learn in this problem how to determine the properties of a spherical capacitor with a varying parmittivity of the dielectric.

Problem Statement

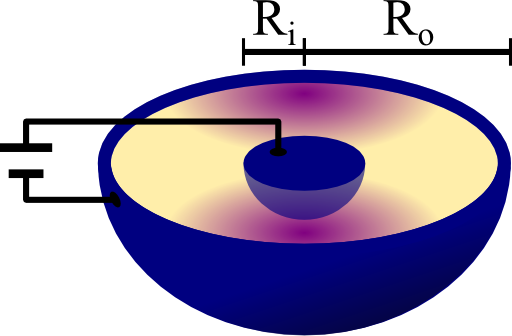Consider a spherical capacitor with inner and outer radii R_i and R_o, respectively. Inside the metallic shells there is a dielectric that with a permittivity ε that may vary with respect to both angles φ and θ.

ε may not change with the radius r. What is the capacitance of such a device? You may want to proceed as follows:

• Calculate first the capacitance when the permittivity is given by:
  
• Compare your result to a spherical capacitor with constant dielectric ε,
  
• Now generalize your calculation for ε(θ,φ). Explain what would be the conceptual difference if the permittivity could also vary on the radius.

Hints

What is the relation between electrostatic potential, charge and capacitance?

Regard the metal/dielectric boundaries. Which condition must the electric field fulfill here?

The problem seems to be complicated at first. However, if you write down the governing equations of the electric field you will have some idea how to tackle it.

Allright, let's jump straight into the solution for the spherical capacitor with varying permittivity!

Solution

We will first calculate the solution for the specified permittivity using Gauss's law in the same way as in "The Coaxial Capacitor with Two Embedded Dielectrics". Having understood this example, we will generalize our result to the angularly varying permittivity.

Specific angular Variation of the Dielectric's Permittivity

The definition of a metal (in electrostatics) tells us that the electric field is always perpendicular to a metallic boundary. Otherwise, charges would flow inside the metal until we find exactly this behavior. Of course this implies a constant electrostatic potential of the metal. Now if we go a little into the dielectric, this must still be true if the dielectric does not vary along the field lines. This would imply surface charges changing the electric field.

For our problem this means that the permittivity may have an angular variation but the electric field still has to be constant for a given radius. And since at the radius of the inner sphere there can only be a radial component this has to be true for the entire capacitor! In mathematical terms

\[\mathbf{E}\left(\mathbf{r}\right) = E_r \left(r\right)\mathbf{e}_r\ ,\]which will hugely simplify our calculations!

Let us consider a spherical Gaussian surface around the inner metallic sphere with radius \(R_i < R < R_o\). Employing the integral formulation of Gauss's law, we find

\[\begin{eqnarray*} Q&=&\int_{\partial V_{R}}\mathbf{D}\left(\mathbf{r}\right)\cdot d\mathbf{A}\\&=&\int_{\partial V_{R}}\varepsilon\left(\theta,\varphi\right)E_{r}\left(R\right)R^{2}\sin\theta d\theta d\varphi\\&=&2\varepsilon_{0}E_{r}\left(R\right)R^{2} \int_{\partial V_{R}}\left(1+\varepsilon_{r}\sin^{2}\varphi\right)d\varphi\\&=&2\varepsilon_{0}E_{r}\left(R\right)R^{2}\left(2\pi+ \pi\varepsilon_{r}\right)\\&=&4\pi\varepsilon_{0}\left(1+\varepsilon_{r}/2\right)E_{r}\left(R\right)R^{2}\ .\end{eqnarray*}\]

Here, \(Q\) is the charge of the inner metallic sphere (not depending on \(R\)). So, for the radial dependence of the electric field we may conclude

\[E_{r}\left(r\right)    =    \frac{1}{4\pi\varepsilon_{0}\left(1+\varepsilon_{r}/2\right)}\frac{Q}{r^{2}}\ . \]

The next step we have to take is to integrate the electric field from inner to outer radius to find how the potential difference relates to the charge. Since the proportional constant is the capacitance, we have almost finished the first task:

\[\begin{eqnarray*} V=\Delta\phi&=&\int_{R_{i}}^{R_{o}}\mathbf{E}\left(\mathbf{r}\right)\cdot d\mathbf{r}\\&=&\int_{R_{i}}^{R_{o}}\frac{1}{4\pi\varepsilon_{0}\left(1+\varepsilon_{r}/2\right)}\frac{Q}{r^{2}}dr\\&=&\frac{Q}{4\pi\varepsilon_{0}\left(1+\varepsilon_{r}/2\right)}\left(\frac{1}{R_{i}}-\frac{1}{R_{o}}\right)\equiv\frac{Q}{C}\ \text{so}\\ C&=&4\pi\varepsilon_{0}\left(1+\varepsilon_{r}/2\right)\frac{R_{i}R_{o}}{R_{o}-R_{i}}\ .  \end{eqnarray*}\]

We of course recover the result for a constant dielectric if \(\varepsilon_{0}\left(1+\varepsilon_{r}/2\right)\rightarrow\varepsilon_{0}\varepsilon_{r}\), i.e. if the part coming from the varying permittivity is replaced by some constant part.

General Permittivities

Now that we know how the capacitance can be calculated for the given example, we may simply stick with a slightly more general formulation for our \(Q\)-integration:

\[\begin{eqnarray*}  Q&=&\int_{\partial V_{R}}\mathbf{D}\left(\mathbf{r}\right)\cdot d\mathbf{A}\\&=&E_{r}\left(R\right)R^{2}\int_{\partial V_{R}}\varepsilon\left(\theta,\varphi\right)d\Omega\equiv E_{r}\left(R\right)R^{2}\int\varepsilon\ . \end{eqnarray*}\]

Then, we directly conclude for the electric field and capacitance

\[\begin{eqnarray*}  E_{r}\left(r\right)&=&\frac{Q}{\int\varepsilon}\frac{1}{r^{2}}\ ,\\C&=&\int\varepsilon\frac{R_{i}R_{o}}{R_{o}-R_{i}}  \end{eqnarray*}\]

as we have done before. So there is really nothing more - only the remaining integration might be quite involved.

If we now had a radial dependence of the permittivity, this would lead to surface charges weakening the electric field. So, in this more general formulation of the problem it might be able to divide the dielectric separation into parts without radial variation since we already know the solution there. For assumed radial jumps of the permittivity we have to use the boundary conditions for the electric field. For a really arbitrary permittivity we might be forced to tackle the problem with numerical methods.