Providing a Homogeneous Magnetic Field - The Helmholtz Coil

Helmholtz coils are a devices that can provide a very homogeneous magnetic field. Although the principle is very old, it is still applied in state-of-the-art experiments. In this problem you will learn how the special characteristics of such coils are achieved.

Problem Statement

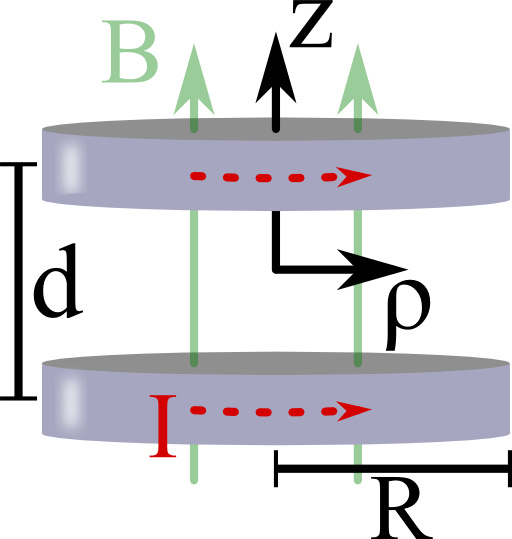
Imagine two coils each of radius R and with current l. Both coils are parallel to each other and separated by a distance d.

Calculate the magnetic induction on the z-axis of symmetry. Find a condition for R and d such that B(z) is as homogeneous in the center between the coils as possible.

Hints

To find the magnetic induction, use the Biot-Savart law.

As homogeneous as possible means that as many spatial derivatives as possible vanish.

Let us straight jump into the solution of this worksheet:

Two Coils: Magnetic Induction

It is useful to first calculate the magnetic induction for a single coil at z = 0 and take a superposition of shifted coils afterwards.

To use the Biot-Savart law

we need to parametrize the curve of the coil.

That means we need to find a mathematical description of each part of the coil's infinitesimal elements. Each element is addressed if a parameter is infinitesimally changed.

One example parametrization example is a circle with radius R. In this case, the angle φ provides a canonical parametrization of the circle.

Ok, let us formulate this in more mathematical terms for the Helmholtz coil!

Using cylindrical coordinates, we find it to be \(\mathbf{r}^{\prime}=R\mathbf{e}_{\rho}\) and \(d\mathbf{r}^{\prime}=R\mathbf{e}_{\varphi}d\varphi\).

So, on the \(z\)-axis we have

\[\begin{eqnarray*}d\mathbf{r}^{\prime}\times\left(z\mathbf{e}_{z}-\mathbf{r}^{\prime}\right)&=&R\mathbf{e}_{\varphi}d\varphi\times\left(z\mathbf{e}_{z}-R\mathbf{e}_{\rho}\right)\\&=&\left(Rz\mathbf{e}_{\rho}+R^{2}\mathbf{e}_{z}\right)d\varphi\ .\end{eqnarray*}\]Because of symmetry, only the \(z\) component of the magnetic induction does not vanish on the \(z\) axis. We calculate it as\[\begin{eqnarray*}B_{z}\left(\rho=0,z\right)&=&\frac{I\mu_{0}}{4\pi}\int\frac{R^{2}d\varphi}{\left(R^{2}+z^{2}\right)^{3/2}}\\&=&\frac{I\mu_{0}}{2}\frac{R^{2}}{\left(R^{2}+z^{2}\right)^{3/2}}\ .\end{eqnarray*}\]Note that we have just the argument \(\rho=0\) explicitly since on the axis \(\mathbf{B}\) cannot depend on \(\varphi\). Then, the magnetic induction of both coils with the same radius and current is given by\[\begin{eqnarray*}B_{z}\left(\rho=0,z\right)&=&\frac{I\mu_{0}R^{2}}{2}\left[\left(R^{2}+\left(z-\frac{d}{2}\right)^{2}\right)^{-3/2}+\left(R^{2}+\left(z+\frac{d}{2}\right)^{2}\right)^{-3/2}\right]\end{eqnarray*}\]where we have chosen the origin of the coordinate system as the center of the coils.

A Condition for Homogeneity

To find a maximal homogeneous field at the center \(z=0\) between the coils, it is useful to expand \(B_{z}\left(\rho=0,z\right)\) as a Taylor series around this point. So, we have to calculate the inner part for which we find\[\begin{eqnarray*}\left(R^{2}+\left(z\pm\frac{d}{2}\right)^{2}\right)^{-3/2}&\approx&\left(R^{2}+\left(\frac{d}{2}\right)^{2}\right)^{-3/2}\mp3\frac{d}{2}\left(R^{2}+\left(\frac{d}{2}\right)^{2}\right)^{-5/2}z\\&&+\frac{3}{2}\left(d^{2}-R^{2}\right)\left(R^{2}+\left(\frac{d}{2}\right)^{2}\right)^{-7/2}z^{2}\mp f\left(R,d\right)z^{3}\ .\end{eqnarray*}\]Hence\[\begin{eqnarray*}\left(R^{2}+\left(z-\frac{d}{2}\right)^{2}\right)^{-3/2}+\left(R^{2}+\left(z+\frac{d}{2}\right)^{2}\right)^{-3/2}&=&2\left(R^{2}+\left(\frac{d}{2}\right)^{2}\right)^{-3/2}\\& & +\,3\left(d^{2}-R^{2}\right)\left(R^{2}+\left(\frac{d}{2}\right)^{2}\right)^{-7/2}z^{2}\ ,\end{eqnarray*}\]plus a small term in \(\mathcal{O}\left(z^{4}\right)\).

Now we can see that the quadratic term in \(z\) vanishes if \(d=R\). This condition makes these two coils a so-called Helmholtz coil named after Hermann von Helmholtz, born in the fabulous city of Potsdam, Germany in 1821. Since the \(z^{3}\)-term in our Taylor-expansion also has a sign change, the magnetic induction is homogeneous in the center up to the fourth derivative! Finally,\[\begin{eqnarray*}B_{z}\left(\rho=0,z\right)&\approx&I\mu_{0}R^{2}\left(R^{2}+\left(\frac{R}{2}\right)^{2}\right)^{-3/2}+\mathcal{O}\left(z^{4}\right)\\&=&\left(\frac{4}{5}\right)^{3/2}\frac{I\mu_{0}}{R}+\mathcal{O}\left(z^{4}\right)\ .\end{eqnarray*}\]

---

Background: Helmholtz Coils - Oldies but Goldies

Helmholtz coils are an old idea but still not at all outdated. One application you might already know is the measurement of the earth's magnetic field. Equivalent to “The Oscillating Dipole Molecule in a Constant Electric Field”, a magnetic dipole like a bar magnet will perform oscillations in a homogeneous magnetic field. The period of oscillation depends on the strength of the magnetic field.

So one can try to cancel the earth's magnetic field using the homogeneous field inside the coils. This cancellation is indicated by an infinite oscillation period. Even with equipment found in high schools this can give reasonable results for the earth's magnetic field. Note that the homogeneity of the field inside the Helmholtz coil is important since otherwise a net force acts on the bar magnet.

Besides these more scholar examples, Helmholtz coils are also found in state-of-the-art experiments. In “Bose-Einstein Condensation of Metastable Helium” by Pereira Dos Santos et al., Physical Review Letters 86 (2001), the authors used a so-called Ioffe-Pritchard-trap to trap a Bose-Einstein condensate made of ultra-cold, excited Helium atoms. Additionally, Helmholtz coils were needed to compensate a field bias inside the trap and increase the confinement of it. So, Helmholtz coils are still of great practical use in highly sophisticated research.

Journal Page | arXiv | PDF