Tags: Image Charges / Dipole
The method of image charges is a powerful technique to find the electrostatic potential in an intuitive way. In this problem you will find out how it can be applied to a point charge close to two grounded intersecting metallic half-planes.
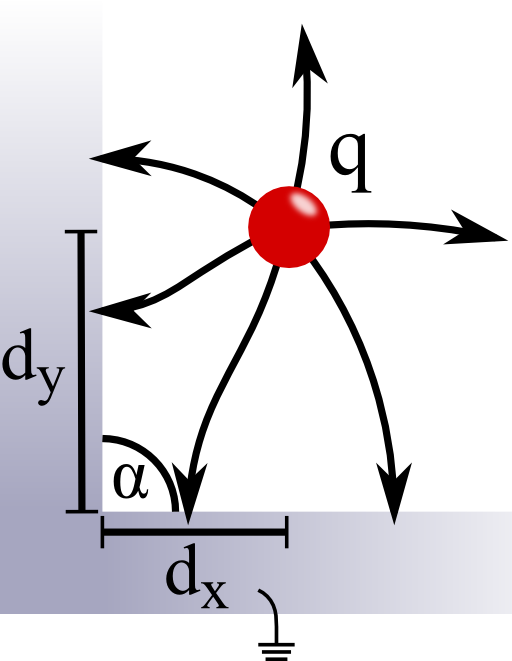
Problem Statement
A point charge q shall be close to two grounded and orthogonal metallic half-planes at rq = (dx, dy, 0).
Calculate the electrostatic potential ϕ(r) and the force acting on the charge using the method of image charges!
Could this method be used if the angle α between the half-planes would be different? Consider the case of α = 60°.
Background: Enhanced Radiation of Molecules
Even if this problem might be very old, we can still learn a lot from it. Imagine for example a molecule in front of a real metal that allows some penetration of the field.
Here, a perfect conductor may still be a very good approximation and one can find the scattered field of the molecule at its very position. This field causes a change of the radiative decay rates of the molecule, a kind of self-induced emission called the Purcell Effect.
This effect is of particular importance to understand applications as the surface enhanced Raman spectroscopy.
Hints
What are the results of the image charge method for a single grounded metal plate?
Can we somehow apply them here with respect to a little more complicated boundary conditions?
Are you able to find the electric field with the help of image charges? Let's move over to the:
Solution
The problem is best tackled using the method of image charges. So, how do we construct the necessary image charges? For a single plate we already know that the charge has to be placed exactly at the opposite position of the metal surface. But here we have two different surfaces, so what can we do? We just have to double the single-plate scenario!
So, let us compensate the charge q at rq = (dx, dy, 0) with two charges -q at \(\mathbf{r}_{-q}^{im,1} = \left(-d_x,d_y,0\right)\) and \(\mathbf{r}_{-q}^{im,2} = \left(d_x,-d_y,0\right)\).
Now this cannot be the solution already since we have overcompensated by two to one charge. To fix this, we place another image charge at \(r_{q}^{im,3} = \left(-d_x,-d_y,0\right)\). Note that this is exactly the position where one would put the image charge to cancel the potential due to the old image charges with respect to the boundaries we did not account for so far. Because of the high symmetry of all charges it is clear that the potential vanishes at the metallic boundaries. The potential outside of the metal is then simply given as the superposition of these charges:
\[\begin{eqnarray}\phi\left(\mathbf{r}\right)&=&\frac{1}{4\pi\epsilon_0}\sum_i \frac{q_i}{\left|\mathbf{r}-\mathbf{r}_i\right|}\ ,\end{eqnarray}\]where now the Index \(i\) stands for all charges.
The force is then calculated using the force of the image charges acting on \(q\):
\[\begin{eqnarray}\mathbf{F}&=&\frac{q^2}{16\pi\epsilon_0}\left(\frac{\mathbf{e}_q}{d_x^2+d_y^2} - \frac{\mathbf{e}_y}{d_y^2} - \frac{\mathbf{e}_x}{d_x^2}\right)\\&=& \frac{q^2}{16\pi\epsilon_0}\left[\left(\frac{d_x}{\left(d_x^2+d_y^2\right)^{3/2}}-\frac{1}{d_x^2}\right)\mathbf{e}_x +\left(\frac{d_y}{\left(d_x^2+d_y^2\right)^{3/2}}-\frac{1}{d_x^2}\right)\mathbf{e}_y\right]\end{eqnarray}\]where \(\mathbf{e}_q\) is a unit vector towards \(q\).
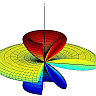
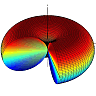
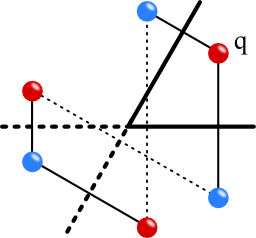Now to \(\alpha = 60^{\circ}\). Here we try the same as before and put image charges at the opposite side of the metal surfaces. We then note that it is a little more complicated to compensate the extra charge. This yields two new image charges which do not coincide.
Thus, we have to find yet another image charge. Luckily, we can compensate it with only one charge again. You can see that this is the crucial point. Using this argumentation one can show that one can only construct the potential using the image charge technique if \(\alpha=180^{\circ}/n\) for some integer \(n\).
Interestingly we found the electrical field just by geometrical considerations! I hope you admire the elegance in this approach.
