Tags: Paul trap / Mathieu differential equation
![]() In this problem we want to understand the mechanism behind ion trapping. We will study the movement of charged particles in a so-called Paul trap by solving the equations of motion using approximative methods.
In this problem we want to understand the mechanism behind ion trapping. We will study the movement of charged particles in a so-called Paul trap by solving the equations of motion using approximative methods.
Problem Statement
Wolfgang Paul received 1989 the Nobel prize in physics for the invention of the so-called Paul trap. Such a device is generally made of three elements of hyperboloidal shape: a ring around the \(z\) axis of symmetry with innermost radius \(\rho_{0}\) and two electrodes starting at \(\pm z_{0}\), see figure below.
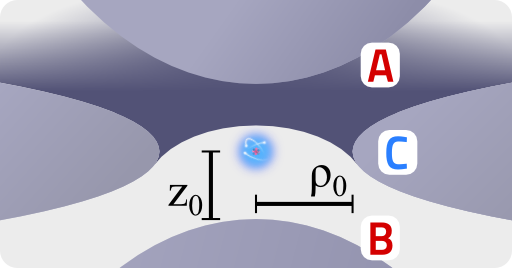
The two electrodes, A and B, are on a different potential than the ring C. Such a configuration yields a quadrupolar electrostatic potential inside the Paul trap:
\[\phi\left(\mathbf{r};t\right) = \phi_{0}\left(t\right)\frac{\rho^{2}-2z^{2}}{\rho_{0}^{2}+2z_{0}^{2}}\ .\]
As we can see, there is an explicit time-dependent function involved, for which we want to assume a slow oscillation with a constant (dc) shift, i.e.
\[\phi_{0}\left(t\right) = U_{\mathrm{dc}}-U_{\mathrm{ac}}\,\cos\left(\Omega t\right)\ .\]
In the following we will convince ourselves that such a potential can indeed be used for ion trapping:
Show that the equations of motion for a charged particle with charge \(q\) and mass \(m\) can be cast in the normal form of a Mathieu differential equation,
\[\frac{d^{2}u\left(\tau\right)}{d\tau^{2}}+\left[a_{u}-2q_{u}\cos\left(2\tau\right)\right]u\left(\tau\right) = 0\ ,\]
for which \(u\in\left\{ \rho,z\right\} \) and identify the dimensionless parameters \(a_{u}\), \(q_{u}\) and \(\tau\).
Find an approximate solution to the Mathieu differential equation for \(U_\mathrm{dc}=0\).
Express the motion of the particle as a superposition of a fast background and slow overall motion of it using
\[u\left(\tau\right) = u_{0}\left(\tau\right)+\delta u\left(\tau\right)\]
with the assumptions
\[\begin{eqnarray*} \left|u_{0}\left(\tau\right)\right|&\gg&\left|\delta u\left(\tau\right)\right|\ \mathrm{and}\\\left|\frac{d^{n}u_{0}\left(\tau\right)}{d\tau^{n}}\right|&\ll&\left|\frac{d^{n}\delta u\left(\tau\right)}{d\tau^{n}}\right|\ \forall n\geq1\ . \end{eqnarray*}\]
Hints
What was the chain rule again?
The characteristic time scales of \(u_{0}\) and \(\delta u\) are strongly different. You should make use of this fact several times!
A differential equation of the form
\[\frac{d^{2}f\left(x\right)}{dx^{2}} = \alpha\left(x\right)\cdot f\left(x\right)\]
may be approximately solved if \(\alpha\) is a much faster varying function than \(f\). Then, one may replace \(\alpha\) by a time-averaged factor.
Ok, let us tame ions inside the Paul trap!
First we will recall how to come bring the ion's equations of motion into the Mathieu form - for every coordinate. After that we will solve the equation approximately to find an oscillatory-like motion inside the Paul trap.
Equations of Motion in Mathieu Form
The potential of a classical Paul or quadrupole trap is given by
\[\begin{eqnarray*} \phi\left(\mathbf{r};t\right)&=&\phi_{0}\left(t\right)\frac{\rho^{2}-2z^{2}}{\rho_{0}^{2}+2z_{0}^{2}}\ ,\ \mathrm{with}\\\phi_{0}\left(t\right)&=&U_{\mathrm{dc}}-U_{\mathrm{ac}}\,\cos\left(\Omega t\right)\ . \end{eqnarray*}\]
The first thing we should discuss is the actual form of the potential. As we can see, if we disregard the time dependence for a moment, \(\phi\) has a saddle point at the origin. So, if there is no time-dependency, we may only achieve trapping in one dimension - a static trapping cannot work! Nevertheless, you might find the time dependency a little odd at this point since we are still in electrostatics.
Strictly speaking, we should state that \(\phi_{0}\left(t\right)\) is slowly varying in a sense that there is no coupling to magnetic or radiation fields and our “electrostatic” description is still a very good approximation. We shall denote this difference by treating the time as a parameter of the potential rather than an actual coordinate.
Let us now try to conclude that the equations of motion are in the form of the "canonical" Mathieu differential equation,
\[\frac{d^{2}u\left(\tau\right)}{d\tau^{2}}+\left[a_{u}-2q_{u}\cos\left(2\tau\right)\right]u\left(\tau\right) = 0\ , \]
where \(u\) is now the \(z\) or \(\rho\) coordinate of the charged particle. Note that each coordinate has additionally assigned parameters \(a\) and \(q\).
To achieve this goal, we of course have to write down the equations of motion. Generally, in our nonrelativistic framework, we have
\[\begin{eqnarray*} m\ddot{\mathbf{r}}\left(t\right)&=&-q\nabla\phi\left(\mathbf{r};t\right)\ .\ \mathrm{so}\\m\ddot{z}\left(t\right)&=&\frac{2q}{\rho_{0}^{2}+2z_{0}^{2}}\,\left[U_{\mathrm{dc}}-U_{\mathrm{ac}}\,\cos\left(\Omega t\right)\right]\, z\left(t\right)\ \mathrm{and}\\m\ddot{\rho}\left(t\right)&=&-\frac{q}{\rho_{0}^{2}+2z_{0}^{2}}\,\left[U_{\mathrm{dc}}-U_{\mathrm{ac}}\,\cos\left(\Omega t\right)\right]\,\rho\left(t\right)\ . \end{eqnarray*}\]
The first thing we have to obviously rescale is the time via
\[\tau = \Omega t/2\ .\]
Then, because of the chain rule,
\[\begin{eqnarray*} \frac{du\left(\tau\left(t\right)\right)}{dt}&=&\frac{du\left(\tau\right)}{d\tau}\frac{d\tau}{dt}=\frac{\Omega}{2}\frac{du\left(\tau\right)}{d\tau}\ ,\\\frac{d^{2}u\left(\tau\left(t\right)\right)}{dt^{2}}&=&\frac{d}{dt}\left[\frac{d}{dt}u\left(\tau\left(t\right)\right)\right]\\&=&\frac{d}{dt}\left[\frac{\Omega}{2}\frac{du\left(\tau\left(t\right)\right)}{d\tau}\right]=\left(\frac{\Omega}{2}\right)^{2}\frac{d^{2}u\left(\tau\right)}{d\tau^{2}}\ , \end{eqnarray*}\]
we obtain the equations of motion in \(\tau\) as
\[\begin{eqnarray*} \ddot{z}\left(\tau\right)-\left(\frac{2}{\Omega}\right)^{2}\frac{2}{\rho_{0}^{2}+2z_{0}^{2}}\frac{q}{m}\,\left[U_{\mathrm{dc}}-U_{\mathrm{ac}}\,\cos\left(2\tau\right)\right]\, z\left(\tau\right)&=&0\ \mathrm{and}\\\ddot{\rho}\left(\tau\right)+\left(\frac{2}{\Omega}\right)^{2}\frac{1}{\rho_{0}^{2}+2z_{0}^{2}}\frac{q}{m}\,\left[U_{\mathrm{dc}}-U_{\mathrm{ac}}\,\cos\left(2\tau\right)\right]\,\rho\left(\tau\right)&=&0\ . \end{eqnarray*}\]
Now we may just read-off the parameters \(a_{u}\) and \(q_{u}\) as
\[\begin{eqnarray*} a_{z}&=&-\left(\frac{2}{\Omega}\right)^{2}\frac{2}{\rho_{0}^{2}+2z_{0}^{2}}\frac{q}{m}U_{\mathrm{dc}}=-2a_{\rho}\ ,\\q_{z}&=&-\left(\frac{2}{\Omega}\right)^{2}\frac{1}{\rho_{0}^{2}+2z_{0}^{2}}\frac{q}{m}U_{\mathrm{ac}}=-2q_{\rho}\ . \end{eqnarray*}\]
Note that for a linear Paul trap with \(\phi_{\mathrm{lin}}\left(\mathbf{r};t\right)\propto x^{2}-z^{2}\), the \(a_{z}\) and \(a_{x}\) are just different by sign; here, the factor "2" comes from our term \(\phi\left(\mathbf{r};t\right)\propto\rho^{2}-{\color{red}2}z^{2}\).
Ok, so far, so good. The last little calculation was merely a technical step. However, this step is very important. Bringing dimensionless parameters into the game often allows to easily identify the main aspects of a theory as well as compare different theories with each other that are mathematically equivalent. Now to the actual physical situation, the solution of the equations of motion and the question if the trapping works.
The Approximate Motion of the Ion
The solution to the Mathieu differential equation is of course known in terms of the Mathieu functions. The general physicist, however, may not be very familiar with these functions. So let's try to understand the movement of the ion in terms of the approximation
\[\begin{eqnarray*} u\left(\tau\right)&=&u_{0}\left(\tau\right)+\delta u\left(\tau\right)\ \mathrm{with}\\\left|u_{0}\left(\tau\right)\right|&\gg&\left|\delta u\left(\tau\right)\right|\ \mathrm{and}\\\left|\frac{d^{n}u_{0}\left(\tau\right)}{d\tau^{n}}\right|&\ll&\left|\frac{d^{n}\delta u\left(\tau\right)}{d\tau^{n}}\right|\ \forall n\geq1\ . \end{eqnarray*}\]
In this way we will learn a lot about characteristic time scales and how we may use them to solve differential equations approximately.
With the simplification of no dc shift, which results in \(a_{z}=a_{\rho}=0\), we find for the Mathieu equation itself
\[\begin{eqnarray*} \frac{d^{2}}{d\tau^{2}}\left[u_{0}\left(\tau\right)+\delta u\left(\tau\right)\right]&=&2q_{u}\cos\left(2\tau\right)\left[u_{0}\left(\tau\right)+\delta u\left(\tau\right)\right]\ ,\ \mathrm{thus}\\\frac{d^{2}\delta u\left(\tau\right)}{d\tau^{2}}&\approx&2q_{u}\cos\left(2\tau\right)u_{0}\left(\tau\right)\ , \end{eqnarray*}\]
where we have adopted the approximations in the second step. Now we can find the solution for the perturbance \(\delta u\left(\tau\right)\) as
\[\delta u\left(\tau\right) \approx -\frac{q_{u}}{2}\cos\left(2\tau\right)u_{0}\left(\tau\right)\ ,\]
since the change in \(u_{0}\left(\tau\right)\) is negligible with respect to the change of the fast oscillations.
We put this result into the Mathieu differential equation and find
\[\begin{eqnarray*} \frac{d^{2}}{d\tau^{2}}\left[u_{0}\left(\tau\right)-\delta u\left(\tau\right)\right]&=&2q_{u}\cos\left(2\tau\right)\left[u_{0}\left(\tau\right)-\frac{q_{u}}{2}\cos\left(2\tau\right)u_{0}\left(\tau\right)\right]\ ,\\\frac{d^{2}u_{0}\left(\tau\right)}{d\tau^{2}}&=&-q_{u}^{2}\cos^{2}\left(2\tau\right)u_{0}\left(\tau\right)\ , \end{eqnarray*}\]
where we have used our earlier result \(\delta u^{\prime\prime}\left(\tau\right)\approx2q_{u}\cos\left(2\tau\right)u_{0}\left(\tau\right)\).
The differential equation we have just derived again leads to Mathieu functions. However, if we look at the nature of the equation, we see that the cosine oscillation is again on another time scale than the movement of \(u_{0}\left(\tau\right)\).
This means that we can integrate out the squared cosine over one period of \(\tau\) in which \(u_{0}\) merely changes. Since \(\int_{0}^{\pi}\cos^{2}\left(2\tau\right)d\tau/\pi=1/2\), we find the approximate differential equation
\[\begin{eqnarray*} \frac{d^{2}u_{0}\left(\tau\right)}{d\tau^{2}}&\approx&-\frac{q_{u}^{2}}{2}u_{0}\left(\tau\right)\ ,\\u_{0}\left(\tau\right)&=&A\cos\left(q_{u}^{2}\tau/2\right) \end{eqnarray*}\]
assuming a cosine-like solution for \(u_{0}\) (generally a superposition of sine and cosine with a discussion of initial values which we may simply omit here). Then we finally have the movement given by
\[\begin{eqnarray*} u\left(\tau\right)&=&u_{0}\left(\tau\right)+\delta u\left(\tau\right)\\&=&A\left(1-\frac{q_{u}}{2}\cos\left(2\tau\right)\right)\cos\left(q_{u}^{2}\tau/2\right)\ ,\ \mathrm{or}\\u\left(t\right)&=&A\underbrace{\left(1-\frac{q_{u}}{2}\cos\left(\Omega t\right)\right)}_{\mathrm{fast\ movement}}\underbrace{\cos\left(q_{u}^{2}\Omega t/4\right)}_{\mathrm{slow\ oscillation}}\ . \end{eqnarray*}\]
We can directly see how the movement has a fast and a slow contribution, provided that \(q_{u}<1\). Most importantly, the movement of the ion is restricted to some region given by the amplitude of the movement which is exactly what an ion trap should be all about!
Background: The numerous Applications of the Paul Trap
We have just calculated that the trapping mechanism really works and hopefully got a basic feeling for the situation. But there is, of course much more to talk about. First of all, if we consider the possible applications of ion traps, the study of fundamental interactions of particles comes to mind. This can be done, since the interaction between different charged particles or to external fields compared to the interaction to the trap itself is generally much stronger.
This principle is employed e.g. in atomic clocks where the trap is an important part that must not change the internal energetic structure of the ions. You can find a very nice explanation of atomic clocks by the 2012 Nobel prize winner David Wineland here. A picture from the lecture below:
Another possibility to use ion traps is to employ them as a mass spectrometer. We haven't talked about this specific issue so far, because this application relies on a certain property of the solutions of the Mathieu equation: Roughly speaking, if the parameters \(a_{u}\) and \(q_{u}\) have certain values, trapping is possible, otherwise the motion is unstable. Now since these parameters directly depend on the mass of the ions and the parameter regions of stability are well-known, the Paul trap can be used as a mass spectrometer! There is a very nice review by Raymond March in the Journal of Mass Spectrometry 32 (1997) “An Introduction to Quadrupole Ion Trap Mass Spectrometry”.
A very convenient introduction to the physics of trapping is also provided in the Nobel lecture by Wolfgang Paul himself entitled “Electromagnetic traps for charged and neutral particles” (1989).