Tags: Resistance / Inductance / Capacitance
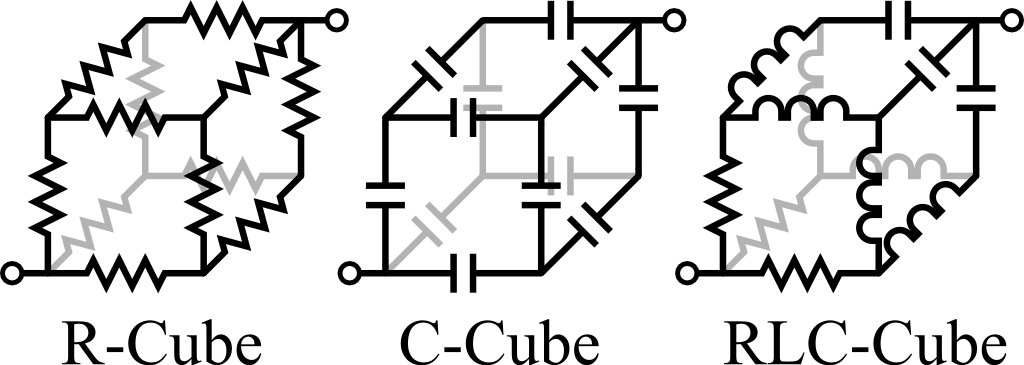
![]() To simplify given circuits is an art of electrical engineers. Often it turns out that a complicated problem seen from a different point of view is extremely easy. The resistance cube ("R-cube") is one such example. The solution we will find can also be used to calculate the impedances of more complicated elements like the "C-cube" or the oscillatory "RLC-cube".
To simplify given circuits is an art of electrical engineers. Often it turns out that a complicated problem seen from a different point of view is extremely easy. The resistance cube ("R-cube") is one such example. The solution we will find can also be used to calculate the impedances of more complicated elements like the "C-cube" or the oscillatory "RLC-cube".
Problem Statement
Find the total resistance Rc of the resistance cube ("R-cube") shown below with respect to opposing edges. You may want to draw a two-dimensional circuit diagram first. There is a lot of redundancy in the cube since all resistances are equal to R - maybe you can find a way to simplify the circuit.
When you have successfully calculated the resistance of the “R-cube”, you can easily calculate the impedance Zc,C of the “C-cube”, where all resistances are exchanged with equal capacitances C. Assume some time-harmonic voltage source connected to the opposing edges.
Can you also find the impedance Zc,RLC of the “RLC-cube” as shown below with resistance R, inducance L and capacitance C?
Hint
If we know that two points in a circuit must have the same voltage, we may short these points without changing anything.
Solution
This problem surely belongs to the class of problems that are extremely tedious to solve if one does not know what to do and starts to throw Kirchhoff's laws at it. Let us make the solution in probably the shortest way possible by looking at the two-dimension circuit of the resistance cube:
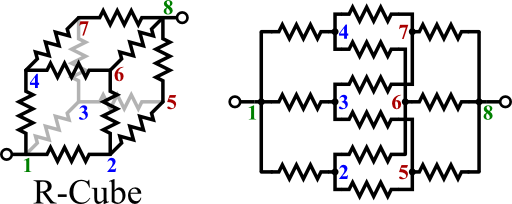
On the left we can see the cube with subsequentially numbered edges, on the right its circuit. Note that intersecting lines are only connected if there is a dot indicating it. The point is, that the voltage at the edges 2-4 (blue) must be equal since we are always connecting equal elements in an equal amount. This also holds for the edges 5-7 (red). Then, we can shorten all blue and red edges to arrive at the following equivalent circuit:
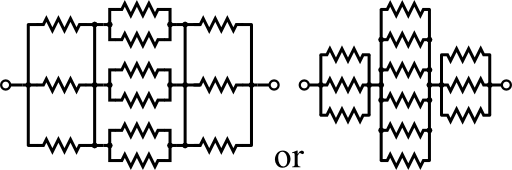
The resistance is then given by the respective parallel resistances, hence
\[R_{c} = \left(\frac{1}{3}+\frac{1}{6}+\frac{1}{3}\right)R=\frac{5}{6}R\ .\]
With this in mind we can directly write down the resistance of the “C-cube” as
\[Z_{c,C} = \frac{5}{6}Z_{C}=\frac{5}{6}\frac{\mathrm{i}}{\omega C}\]
since we only replaced certain equal impedances.
The “RLC-cube” is arranged in a manner that the same simplification can be done as before: Even if not all elements in the circuit are equal, the resistors are connected to equal inductances and those are connected to equal capacitances. Hence the equivalent circuit is given by
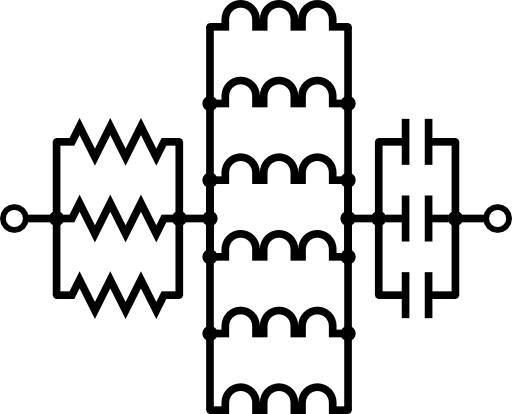
So we find
\[Z_{c,RLC} = \frac{1}{3}R+\frac{1}{6}Z_{L}+\frac{1}{3}Z_{C}=\frac{1}{3}R-\frac{1}{6}\mathrm{i}\omega L+\frac{1}{3}\frac{\mathrm{i}}{\omega C}\]
which is the impedance of a Serial RLC Circuit.
Again, geometrical considerations have helped us drastically!