Tags: Rotational Symmetry / Quadrupole Moment / Legendre Polynomials
![]() We will calculate the first three multipole moments of a deformed charged sphere. Such a charge distribution is often used to model nuclei and understand their stability. The rotational symmetry of the problem will ease our computations significantly.
We will calculate the first three multipole moments of a deformed charged sphere. Such a charge distribution is often used to model nuclei and understand their stability. The rotational symmetry of the problem will ease our computations significantly.
Problem Statement
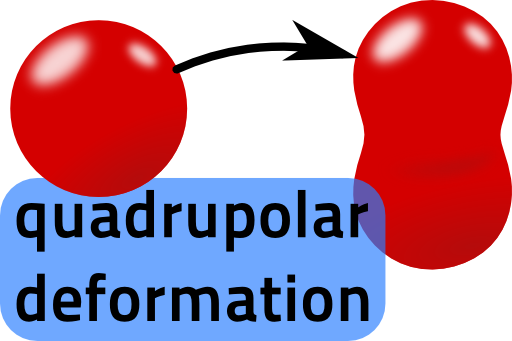
Calculate the first three multipole moments of a slightly deformed sphere with homogeneous charge distribution ρ(r) as depicted on the right.
Mathematically, the surface of the deformed sphere is paramtrized by
\[R\left(\theta,\varphi\right) = R_{0}\left(1+\xi P_{2}\left(\cos\theta\right)\right)\ ,\]
with the Legendre polynomial of second order,
\[P_{2}\left(\cos\theta\right)=\left(3x^{2}-1\right)/2\ .\]
Assume that the deformation parameter ξ ≪ 1 and calculate ρ's total charge, dipole moment and quadrupole moment approximately in leading order of ξ.
Note that in rotational symmetry we have to calculate only one moment per order as discussed in "Multipole Moments in Rotational Symmetry".
We use the second order Legendre polynomial to achieve the deformation. This order is naturally linked to the quadrupole moment. So we could say that the deformation itself is of "quadrupolar nature". Shortly discuss if this kind of deformation implies that higher order multipole moments vanish.
Hints
Remember that
\[\begin{eqnarray*} \left(1+x\right)^{m}&\approx&1+mx+\frac{1}{2}m\left(m-1\right)x^{2}\\&&+\frac{1}{6}m\left(m-1\right)\left(m-2\right)x^{3}+\mathcal{O}\left(x^{4}\right) \end{eqnarray*}\]
might be a quite useful expansion for some \(x\ll1\).
The Legendre Polynomials are not orthonormal but rather “only” orthogonal. Their inner product yields
\[\begin{eqnarray*} \int_{-1}^{1}P_{n}\left(x\right)P_{m}\left(x\right)dx&=&\frac{2}{2n+1}\delta_{nm}\ \mathrm{for}\\P_{0}\left(x\right)&=&1\\P_{1}\left(x\right)&=&x\\P_{2}\left(x\right)&=&\frac{1}{2}\left(3x^{2}-1\right)\ \mathrm{etc.} \end{eqnarray*}\]
Don't forget that symmetries may render some calculations unnecessary.
These were quite some mathematical hints on series expansions, Legendre polynomials and symmetries. Can you make use of them to find the quadrupole moment of the deformed sphere?
Solution
Let us first remember how to calculate multipole moments for rotational symmetry. Then we will specify the general formulation to the deformed sphere and use our findings to determine the multipole moments of it.
Multipole Moments in Rotational Symmetry
In "Multipole Moments in Rotational Symmetry" we have calculated that the electrostatic potential in rotational symmetry is given by
\[\phi\left(r,\theta\right) = \frac{1}{4\pi\varepsilon_{0}}\sum_{l=0}^{\infty} \frac{b_{l}P_{l} \left( \cos\theta\right)}{r^{l+1}}\]
with the multipole moments \(b_{l}\) calculated via
\[b_{l} = \int P_{l}\left(\cos\theta^{\prime}\right)r^{\prime l}\rho\left(r^{\prime},\theta^{\prime}\right)dV^{\prime}\ .\]
The main message was that in rotational symmetry there is only one multipole per order \(l\) to fully characterize the electrostatic potential away from the sources. Even though this description might sound restricitive, it allows to understand a lot of physics.
The Multipole Moments of the Deformed Sphere
For this problem, we have the charge distribution formally given by
\[\rho\left(\mathbf{r}\right) = \rho_{0}\Theta\left(R_{0}\left(1+\xi P_{2}\left(\cos\theta\right)\right)-r\right)\ ,\]
which is a deviation from the homogeneously charged sphere (which we have already calculated in "The Electric Field and Potential of a Homogeneously Charged Sphere"). We have assumed that the deformation is small, i.e. the dimensionless parameter \(\xi\ll1\).
All we have to do to calculate the multipole moments is to solve the equation for the \(b_{l}\):
\[\begin{eqnarray*} b_{l}&=&\int P_{l}\left(\cos\theta^{\prime} \right)r^{\prime l}\rho\left(r^{\prime},\theta^{\prime}\right)dV^{\prime}\ \\&=&\rho_{0}\int P_{l}\left(\cos\theta^{\prime}\right)r^{\prime l}\Theta\left(R_{0}\left(1+\xi P_{2}\left(\cos\theta\right)\right)-r^{\prime}\right)r^{\prime2}\sin\theta drd\theta d\varphi\\&=&2\pi\rho_{0}\frac{R_{0}^{l+3}}{l+3}\int_{0}^{\pi}P_{l}\left(\cos\theta^{\prime}\right)\left(1+\xi P_{2}\left(\cos\theta^{\prime}\right)\right)^{l+3}\sin\theta d\theta \end{eqnarray*}\]
where we have performed the \(\varphi\) and \(r\) integration.
Remember that we switch the order of integration by the virtue of Fubini's theorem.
So far, we have not used that the deformation is small. However, in this still rather general form, the integration is quite hard to tackle and we may not simply use the orthogonality of the Legendre polynomials. With respect to the expansion outlined in the hints, the multipole moments are for small \(\xi\) given by
\[\begin{eqnarray*} b_{l}& = &2\pi \rho_{0}\frac{R_{0}^{l+3}}{l+3}\int_{-1}^{1}P_{l} \left(x\right)\left(1+\xi P_{2} \left(x\right)\right)^{l+3}dx\\& \approx &2\pi \rho_{0}\frac{R_{0}^{l+3}}{l+3}\int_{-1}^{1}P_{l}\left(x\right) \cdot\\&&\left(1+ \left(l+3\right)\xi P_{2}\left(x\right)+\frac{1}{2}\left(l+3\right)\left(l+2\right)\xi^{2}P_{2}\left(x\right)^{2}\right)dx \ ,\end{eqnarray*}\]
where we have also changed the integration over \(\theta\) to the variable \(x\) for a shorter notation.
Now we are set up and can simply use the latter equation to calculate the multipole moments.
The Charge of the Deformed Sphere
Using our derived formulation, we can calculate the total charge via
\[b_{0} \approx 2\pi\rho_{0}\frac{R_{0}^{3}}{3}\int_{-1}^{1}P_{0}\left(x \right)\cdot\left(1+3\xi P_{2} \left(x\right)+3\xi^{2}P_{2} \left(x\right)^{2}\right)dx\]
Now we can see that because of the orthogonality of the Legendre polynomials we only have to consider the squared term and use \(\int P_{2}\left(x\right)^{2}dx=2/5\). Then, we end up with
\[\begin{eqnarray*} b_{0}& \approx & 2 \pi\rho_{0}\frac{R_{0}^{3}}{3}\int_{-1}^{1}1+\frac{3}{4} \xi^{2}x^{2}dx\\& = &2\pi \rho_{0}\frac{R_{0}^{3}}{3} \left(2+3\frac{2}{5}\xi^{2}\right)\\&=&\rho_{0}V_{s}^{0} \left(1+\frac{3}{5}\xi^{2}\right)\ \mathrm{with}\\V_{s}^{0}& = &\frac{4\pi}{3}R_{0}^{3} \end{eqnarray*}\]
as the volume of the deformed sphere. This result is exactly what we would have expected - the total charge changes slightly because of the increased volume.
The Dipole Moment
We will not calculate this moment explicitly simply because we don't have to. The reason is that the deformation of the sphere is even in \(\theta\) with respect to \(\theta=\pi/2\) - we have a mirror symmetry in the \(xy\)-plane in addition to the rotational symmetry. That means: there cannot be a dipole moment, any deformation is not in “one direction” as it would be necessary for a dipole moment. Hence,\[b_{1} = 0\ .\]
The Quadrupole Moment
To calculate the quadrupole moment, we have to come back to the actual formulas. Within our approximation, we write note
\[\begin{eqnarray*} b_{2}& \approx&2\pi\rho_{0}\frac{R_{0}^{5}}{5}\int_{-1}^{1}P_{2} \left(x\right)\cdot\\& &\left(1+5\xi P_{2}\left(x\right)+\frac{1}{2}\cdot5\cdot4\cdot \xi^{2}P_{2}\left(x\right)^{2}\right)dx\ . \end{eqnarray*}\]
Now we see that the \(1\equiv P_{0}\left(x\right)\) doesn't contribute to the integral, but already the first term in \(\xi\) does. Using again \(\int P_{2}\left(x\right)^{2}dx=2/5\), we find
\[\begin{eqnarray*} b_{2}&\approx&2\pi\rho_{0}R_{0}^{5}\,\frac{2}{5}\xi\\&=&\frac{3}{5}\rho_{0}V_{s}^{0}R_{0}^{2}\xi\ . \end{eqnarray*}\]
If we did not miscalculate, this is our astonishingly simple result.
Higher Order Multipole Moments
Now what about higher order multipole moments? If we look once again at the integration we had to perform to find the multipole moments, say without the \(\xi\)-expansion, we fastly realize that there will be infinitely many higher order multipole moments. This is true with and without approximation - in either case we will have the second order Legendre polynomial to a certain exponent which will contribute to higher moments.
A further analysis reveals that there will exist only even multipole moments to any order and that \(b_{2l}\sim\xi^{l}\) in the lowest order of \(\xi\). So it is not true, that such a quadrupolar deformation just results in a quadrupole moment! Please keep this in mind as it is a common misconception that somehow “simple” shaped bodies only have certain low-order multipole moments!
Background: From Electrostatics to Nuclear Physics - the Stability of Nuclei
Nowadays we are celebrating the proof of the Higgs boson, which was found using huge laboratories and enormous efforts to handle the enormous amounts of created data. These results are basically the proof of the standard model and physicists around the world are eager to find even more in-depth questions requiring even more sophisticated methods to verify. But of course these findings are at the end of a long journey of humans to understand the nature of the fundamental particles.
 When Robert Hofstadter, an American physicist (Nobel prize 1961), started to make huge contributions to the understanding of the structure of nuclei, it was widely believed that these tiny things did not have any inner structure. Knowledge has advanced and we can perform scattering experiments to reveal nuclei machinery. Their charge distribution can be approximated by a sharp boundary
When Robert Hofstadter, an American physicist (Nobel prize 1961), started to make huge contributions to the understanding of the structure of nuclei, it was widely believed that these tiny things did not have any inner structure. Knowledge has advanced and we can perform scattering experiments to reveal nuclei machinery. Their charge distribution can be approximated by a sharp boundary
\[R\left(\theta\right) = R_{0}\left(1+\xi_{2}P_{2}\left(\cos\theta\right)+\xi_{4}P_{4}\left(\cos\theta\right)\right)\ ,\]
very similar to the charge distribution we made ourself familiar with.
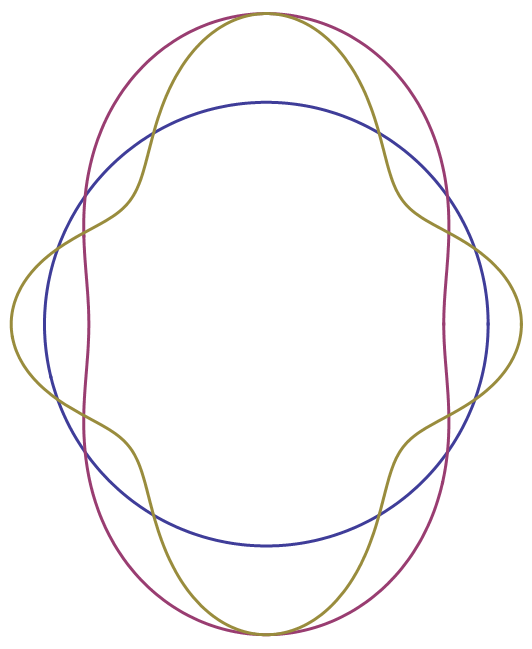
On the right you can see contour plots of spheres with different kinds of deformation - no (blue), quadrupolar (magenta) and octupolar (yellow). The deformation parameters \(\xi_{i}\) are in direct relation to the stability of a nucleus. If the quadrupole- and octadupole deformation parameters \(\xi_{1}\) and \(\xi_{2}\) are small, the nucleus is close to spherical symmetry.
Such nuclei are extremely stable, examples are \(^{4}\text{He}\) and \(^{208}\text{Pb}\). Unstable elements with larger deformation parameters are the rare earths or the actinoides including \(^{238}\text{U}\). The reason behind the stability is the binding energy. The higher it is, the more favorable is a symmetric shape.
For smaller binging energies, repulsive forces inside the nucleus are considerable and thus lead to the described deformations. In the end, if one can measure the measurement of multipole moments thus gives a fundamental insight into their inner structure - electrostatics takes an important place to understand matter even in times of the Higgs boson!
Further reading
You may enjoy the MIT open courseware lectures on applied nuclear physics, link (a basic understanding of quantum mechanics will be necessary).
Writtin in a more popular style is the freely available book “Nucleus - a trip in the heart of matter”.