The Electric Field of a Dipole

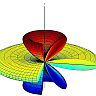
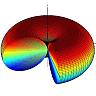
The electric field of a dipole can be seen as the result of two charges approaching each other. Learn in this problem how to use the Taylor expansion of 1/|r-r'| to calculate this field. Find out how this series expansion yields multipole moments, a very powerful description of the electric field.

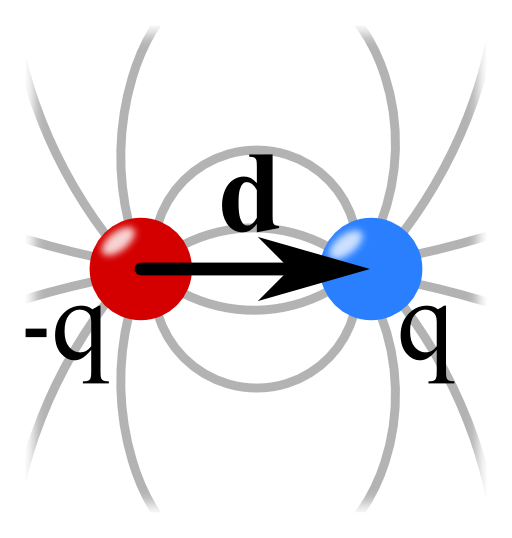
Problem Statement

Find the electric field of an electric dipole using the following steps:

• Find the electrostatic potential of two point charges \(q_{1/2}=\pm q\) at \(\mathbf{r}_{1/2}=\pm\frac{1}{2}\mathbf{d}\).
• Take the limit \(\left|\mathbf{d}\right|\rightarrow0\) of the potential holding \(\mathbf{p}:=q\mathbf{d}\) constant.
• Calculate the electric field from the electrostatic potential.
• additional: Verify that the following charge distribution yields the correct dipole potential

\[\rho\left(\mathbf{r}\right)=-\mathbf{p}\cdot\nabla\delta\left(\mathbf{r}\right)\]

Background: The Dipole as Limiting Process

As we have found in The Electric Field of two Point Charges, the electric field of two opposite charges is fundamentally different from that of a single charge decreasing with \(1/r^{3}\) at large distances, not only with \(1/r^{2}\).

This is not just a coincidence but stems from the so-called multipole expansion as we have outlined earlier.

For now, let us try to find the dipole term by the limiting process of the given problem!

Hints

The electrostatic potential of a point charge is given by (see again The Electric Field of a Point Charge)

\[\phi\left(\mathbf{r}\right) = \frac{1}{4\pi\varepsilon_{0}}\frac{q}{\left|\mathbf{r}-\mathbf{r}_{q}\right|}\ .\]

How can you calculate the field for several point charges?

Look at the arising potential for two charges. If you just insert \(\mathbf{d}=0\), \(\phi\left(\mathbf{r}\right)\) will simply vanish.

Try to consider \(\phi\left(\mathbf{r}\right)\) in terms of a series expansion in \(\mathbf{d}\) to find its dependence of this parameter!

What is the relation between electrostatic field \(\mathbf{E}\left(\mathbf{r}\right)\) and the electrostatic potential \(\phi\left(\mathbf{r}\right)\)?

For the additional part of of the problem, you will have to derive the \(\delta\)-distribution. Generally, acting on a test function \(\varphi\), the derivative of a distribution is given by partial integration:

\[\int_{\mathbb{R}}\delta^{\prime}\left(x\right)\varphi\left(x\right)dx = -\int_{\mathbb{R}}\delta\left(x\right)\varphi^{\prime}\left(x\right)dx=-\varphi^{\prime}\left(0\right)\ .\]

As you can see this problem is quite interesting! What will happen if we now mathematically combine the opposing charges? Find it out in the solution section!

Solution

The main steps to find the solution to this problem are first to figure out the electrostatic potential \(\phi\left(\mathbf{r}\right)\) for a finite separation of the two charges. Then we have to use a Taylor expansion of the potential for small separations which will be outlined in detail. This will directly lead us to the potential of a dipole and its electric field.

The electrostatic potential for the two charges is given by a superposition of the potentials of each charge alone,

\[\begin{eqnarray*}\phi\left(\mathbf{r}\right)&=&\frac{1}{4\pi\varepsilon_{0}}\frac{q_{1}}{\left|\mathbf{r}-\mathbf{r}_{1}\right|}+\frac{1}{4\pi\varepsilon_{0}}\frac{q_{2}}{\left|\mathbf{r}-\mathbf{r}_{2}\right|}\\ & = &\frac{q}{4\pi\varepsilon_{0}}\left\{\frac{1}{\left|\mathbf{r}-\frac{1}{2}\mathbf{d}\right|}-\frac{1}{\left|\mathbf{r}+\frac{1}{2}\mathbf{d}\right|}\right\} \ .\end{eqnarray*}\]

We now have to expand this potential in a Taylor series around \(\mathbf{d}=0\). But let's take the chance to look at the Taylor expansion once again.

The Taylor expansion of \(1/\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\)

Remember that under certain assumptions of convergence, the Taylor expansion for a scalar function of one variable is given by \[\begin{eqnarray*} f\left(x\right) & = & f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{1}{2}f^{\prime\prime}\left(x_{0}\right)\left(x-x_{0}\right)^{2}+\dots\\& = & \sum_{n=0}^{\infty}\frac{1}{n!}\left.\frac{d^{n}f\left(x\right)}{dx^{n}}\right|_{x_{0}}\cdot\left(x-x_{0}\right)^{n}\ ,\end{eqnarray*}\] or, in another familiar form as \[\begin{eqnarray*}f\left(x-x_{0}\right) & = & \sum_{n=0}^{\infty}\frac{1}{n!}\left.\frac{d^{n}f\left(x-x_{0}\right)}{dx^{n}}\right|_{x=0}x^{n}\end{eqnarray*}\] using a little shift in the coordinate. For a function depending on several variables, it is better to use a notation with indices. For example with \(x_{1}=x\), \(x_{2}=y\) and \(x_{3}=z\) we have (around \(\mathbf{r}^{\prime}\)) \[\begin{eqnarray*}f\left(\mathbf{r}-\mathbf{r}^{\prime}\right) & = & f\left(\mathbf{r}\right)+\left.\frac{\partial f\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}{\partial x_{1}}\right|_{\mathbf{r}=0}x_{1}+\\& & \left.\frac{\partial f\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}{\partial x_{2}}\right|_{\mathbf{r}=0}x_{2}+\left.\frac{\partial f\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}{\partial x_{3}}\right|_{\mathbf{r}=0}x_{3}\\& & +\mathcal{O}\left(\mathbf{r}^{2}\right)\end{eqnarray*}\]using the second form of the Taylor expansion.

Here, however, we need an expansion of the potential around \(\mathbf{d}=0\). So we have to treat \(\mathbf{d}\) as the variable! To do so, we need an expansion of the function \(1/\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\) around \(\mathbf{r}^{\prime}=0\) since the terms basically have this form with \(\mathbf{r}^{\prime}=\pm\frac{1}{2}\mathbf{d}\). \[\begin{eqnarray*}\frac{1}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} & = & \frac{1}{\sqrt{\sum_{n=1}^{3}\left(x_{n}-x_{n}^{\prime}\right)^{2}}}\\& = & \left(\sum_{n=1}^{3}\left(x_{n}\right)^{2}\right)^{-1/2}+\sum_{k=1}^{3}\frac{\partial}{\partial x_{k}^{\prime}}\left. \left(\sum_{n=1}^{3}\left(x_{n}-x_{n}^{\prime}\right)^{2}\right)^{-1/2}\right|_{x_{k}^{\prime}=0}x_{k}^{\prime}+ \mathcal{O}\left(\mathbf{r^{\prime}}^{2}\right)\\& = & \frac{1}{r}+\sum_{k=1}^{3}\left.\left(-\right)2\left(x_{k}-x_{k}^{\prime}\right)\cdot\left(-\right)\frac{1}{2}\left(\sum_{n=1}^{3}\left(x_{n}-x_{n}^{\prime}\right)^{2}\right)^{-3/2} \right|_{x_{k}^{\prime}=0}x_{k}^{\prime}+\mathcal{O}\left(\mathbf{r^{\prime}}^{2}\right)\\& = & \frac{1}{r}+\frac{1}{r^{3}}\sum_{k=1}^{3}x_{k}x_{k}^{\prime}+\mathcal{O}\left(\mathbf{r^{\prime}}^{2}\right)=\frac{1}{r}+\frac{\mathbf{r}\cdot\mathbf{r}^{\prime}}{r^{3}}+\mathcal{O}\left(\mathbf{r^{\prime}}^{2}\right)\ .\end{eqnarray*}\]Here we have used the chain rule \(\frac{d}{dx}\left(f\circ g\right)\left(x\right)=f^{\prime}\left(g\left(x\right)\right)g^{\prime}\left(x\right)\). Note that it is also possible to derive this result using \(\frac{\partial}{\partial x_{k}^{\prime}}1/\left|\mathbf{r}-\mathbf{r}^{\prime}\right|=-\frac{\partial}{\partial x_{k}}1/\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\) as you may come across in the literature.

Calculating the Electrostatic Potential and the Electric Field

We can apply our found expansion of the function \(1/\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\) using \(\mathbf{r}^{\prime}\rightarrow\pm\frac{1}{2}\mathbf{d}\) to get an expression of the dipole potential for small separations: \[\begin{eqnarray*}\frac{4\pi\varepsilon_{0}}{q}\phi\left(\mathbf{r}\right) & = & \frac{1}{\left|\mathbf{r}-\frac{1}{2}\mathbf{d}\right|}-\frac{1}{\left|\mathbf{r}+\frac{1}{2}\mathbf{d}\right|}\\& = & \frac{1}{r}+\frac{1}{2}\frac{\mathbf{d}\cdot\mathbf{r}}{r^{3}}-\frac{1}{r}+\frac{1}{2}\frac{\mathbf{d}\cdot\mathbf{r}}{r^{3}}+\mathcal{O}\left(\mathbf{d}^{2}\right)\\& = & \frac{\mathbf{d}\cdot\mathbf{r}}{r^{3}}+\mathcal{O}\left(\mathbf{d}^{2}\right)\ .\end{eqnarray*}\]Now, we can perform the limit \(\mathbf{d}\rightarrow0\) holding \(\mathbf{p}=q\mathbf{d}\) constant to find the potential of a dipole as \[\begin{eqnarray*}\phi\left(\mathbf{r}\right) & = & \frac{1}{4\pi\varepsilon_{0}}\frac{\mathbf{p}\cdot\mathbf{r}}{r^{3}}\ .\end{eqnarray*}\] Ok, we have made some nice progress up to now. We found the dipole potential from the somehow technical but extremely useful Taylor expansion of \(1/\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\). But we can still go a step further and calculate the electric field using \(\mathbf{E}\left(\mathbf{r}\right)=-\nabla\phi\left(\mathbf{r}\right)\).

Now there is a long way to come to the desired result and a somewhat shorter one. The long way is to use that \[ \begin{eqnarray*}\frac{\mathbf{p}\cdot\mathbf{r}}{r^{3}} & = & -\mathbf{p}\cdot\nabla\frac{1}{r}\end{eqnarray*}\ ,\]treat this product as vector product and use certain identities from vector calculus. I don't particularly like this. On the other hand we can also view \(\phi\left(\mathbf{r}\right)\) as a product of scalar functions, namely \(\mathbf{p}\cdot\mathbf{r}\) and \(r^{-3}\). Then we know that \(\nabla\left(\mathbf{p}\cdot\mathbf{r}\, r^{-3}\right)=\mathbf{p}\cdot\mathbf{r}\nabla r^{-3}+r^{-3}\nabla\mathbf{p}\cdot\mathbf{r}\). For the second term we see that \(\nabla\mathbf{p}\cdot\mathbf{r}=\mathbf{p}\), since \(\mathbf{p}\) is a constant vector. The other term is a little bit harder. In cartesian coordinates we calculate \[\begin{eqnarray*} \nabla\frac{1}{r^{3}} & = & \underbrace{\sum_{i}\mathbf{e}_{i}\frac{\partial}{\partial x^{i}}}_{=\nabla}\underbrace{\left(\sum_{n}x_{n}^{2} \right)^{-3/2}}_{=r^{-3}}\\ & = & \sum_{i}\mathbf{e}_{i}2\delta_{in}x_{n}\left(-\frac{3}{2}\right)\left(\sum_{n}x_{n}^{2}\right)^{-5/2}\\ & = & -3\frac{\mathbf{r}}{r^{5}} \end{eqnarray*}\]applying the chain rule.

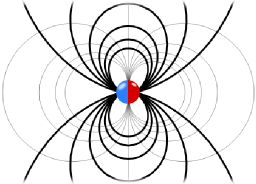Putting everything together finally yields \[\begin{eqnarray*}\mathbf{E}\left(\mathbf{r}\right) & = & -\nabla\phi\left(\mathbf{r}\right)=\frac{1}{4\pi\varepsilon_{0}}\left[3\left(\mathbf{p}\cdot\mathbf{r}\right)\frac{\mathbf{r}}{r^{5}}-\frac{\mathbf{p}}{r^{3}}\right]\ .\end{eqnarray*}\]Note that this field is sometimes called a "mathematical dipole" and you might guess the reason for it. In the Taylor expansion we were just taking the linear term in \(\mathbf{d}\). We have neglected all higher order terms. So the field we just found is a certain kind of approximation for distances larger than the dipole separation. We always have to remember how we came to a certain solution - the electric field will definately be different close to the dipole, see again The Electric Field of two Point Charges.

Verification of \(\rho\left(\mathbf{r}\right)=-\mathbf{p}\cdot\nabla\delta\left(\mathbf{r}\right)\)

As given in the hints, we have to use the derivation of the \(\delta\) distribution here. In one dimension it is given by\[\int_{\mathbb{R}}\delta^{\prime}\left(x\right)\varphi\left(x\right)dx = -\int_{\mathbb{R}}\delta\left(x\right)\varphi^{\prime}\left(x\right)dx = -\varphi^{\prime}\left(0\right)\ ,\]but we may apply this rule directly in three dimension since the result is the same. Ok, taking the integral formulation of Gauss's law\[\begin{eqnarray*}\phi\left(\mathbf{r}\right)&=&\frac{1}{4\pi\varepsilon_{0}}\int\frac{\rho\left(\tilde{\mathbf{r}}\right)}{\left|\mathbf{r}-\tilde{\mathbf{r}}\right|}d\tilde{V} \\ &=& \frac{1}{4\pi\varepsilon_{0}}\int\frac{-\mathbf{p}\cdot\nabla_{\tilde{\mathbf{r}}}\delta\left(\tilde{\mathbf{r}}\right)}{\left|\mathbf{r}-\tilde{\mathbf{r}}\right|}d\tilde{V} \\ &=& \frac{1}{4\pi\varepsilon_{0}}\int\delta\left(\tilde{\mathbf{r}}\right)\mathbf{p}\cdot\nabla_{\tilde{\mathbf{r}}}\frac{1}{\left|\mathbf{r}-\tilde{\mathbf{r}}\right|}d\tilde{V} \\ &=& \frac{1}{4\pi\varepsilon_{0}}\int\delta\left(\tilde{\mathbf{r}}\right)\mathbf{p}\cdot\frac{\mathbf{r}-\tilde{\mathbf{r}}}{\left|\mathbf{r}-\tilde{\mathbf{r}}\right|^{3}}d\tilde{V} \\ &=& \frac{1}{4\pi\varepsilon_{0}}\frac{\mathbf{p}\cdot\mathbf{r}}{r^{3}}\ .\end{eqnarray*}\]

Note that \(\mathbf{p}\) is just a constant vector such that \(\nabla_{\tilde{\mathbf{r}}}\mathbf{p}f\left(\tilde{\mathbf{r}}\right)=\mathbf{p}\cdot\nabla_{\tilde{\mathbf{r}}}f\left(\tilde{\mathbf{r}}\right)\). Furthermore it is crucial here to take the derivative with respect to the coordinate of the charge distribution, \(\tilde{\mathbf{r}}\)! Otherwise we would get a sign change for the potential.

The verification of this charge distribution for a dipole is very useful. It provides a relation between the polarization of a dielectric object,\[\mathbf{P}\left(\mathbf{r}\right) = \sum_{d}\mathbf{p}_{d}\delta\left(\mathbf{r}-\mathbf{r}_{d}\right)\]and the charge density:\[\begin{eqnarray*}\rho\left(\mathbf{r}\right)&=&-\sum_{d}\mathbf{p}_{d}\nabla\delta\left(\mathbf{r}-\mathbf{r}_{d}\right)\\&=&-\nabla\sum_{d}\mathbf{p}_{d}\delta\left(\mathbf{r}-\mathbf{r}_{d}\right)\\&=&-\nabla\mathbf{P}\left(\mathbf{r}\right)\ .\end{eqnarray*}\]This relation will be extremely useful for our understanding of dielectric media in external electric fields.

It is worthwile to reconsider the dipole as the second most "simple" charge configuration we can think of. And even this very basic electrostatic configuration has given us many insights on electrical fields. We will have a great use of these findings in the antenna theory section, in which we hugely rely on our electrostatic understanding.