![]() The so-called boundary integral equation relates the values of the electrostatic potential in some domain to its values at that domain's boundary. In this problem we will derive this important statement which leads to the "Boundary Element Method", a discretized version with numerical applications throughout science and engineering.
The so-called boundary integral equation relates the values of the electrostatic potential in some domain to its values at that domain's boundary. In this problem we will derive this important statement which leads to the "Boundary Element Method", a discretized version with numerical applications throughout science and engineering.
Problem Statement
Derive the boundary integral equation for a region Ω containing no charges:
- Given the Poisson equation for a function \(u\left(\mathbf{r}\right)\), \(\Delta u\left(\mathbf{r}\right)=0\) in some domain Ω and likewise for \(w\left(\mathbf{r}\right)\), derive Green's second identity
\[\int_{\Omega}u\left(\mathbf{r}\right)\Delta w\left(\mathbf{r}\right)dV-\int_{\Omega}w\left(\mathbf{r}\right)\Delta v\left(\mathbf{r}\right)dV = \int_{\partial\Omega}\left[u\left(\mathbf{r}\right)\partial_{\boldsymbol{\mathbf{\nu}}}w\left(\mathbf{r}\right)-w\partial_{\boldsymbol{\mathbf{\nu}}}u\left(\mathbf{r}\right)\right]d\mathbf{A}\ .\] - Now derive the actual boundary integral equation: Green's function for the Laplace operator is defined by \(\Delta G\left(\mathbf{r},\mathbf{r}^{\prime}\right)=\delta\left(\mathbf{r}-\mathbf{r}^{\prime}\right)\). Apply Green's second identity now for the electrostatic potential \(\phi\left(\mathbf{r}\right)\) and \(G\left(\mathbf{r},\mathbf{r}^{\prime}\right)\).
- Regarding the boundary integral equation, can you imagine what kind of problem may arise if one uses it in a numerical implementation?
Hints
What was again the divergence theorem?
Putting the electrostatic potential into Green's second identity, can you make use of Gauss's law?
Ok, let us derive the boundary integral equation!
Greens Second Identity
The fundamental equation of the boundary integral equation is Green's second identity. We will derive it in the following.
Let us assume two scalar functions \(u\left(\mathbf{r}\right)\) and \(w\left(\mathbf{r}\right)\) sufficiently smooth that we can perform all coming steps. The goal is to rewrite \(\int_{\Omega}u\left(\mathbf{r}\right)\Delta w\left(\mathbf{r}\right)dV-\int_{\Omega}w\left(\mathbf{r}\right)\Delta v\left(\mathbf{r}\right)dV\) in terms of a surface integral. Since the relation also holds for the Helmholtz equation where \(\Delta\) is replaced by \(\Delta+k^{2}\), we can do the derivation here with respect to the operator \(\Delta+k^{2}\). It is sufficient to calculate only one term and take the difference afterwards. Remember that \(\Delta f\left(\mathbf{r}\right)=\nabla\cdot\nabla f\left(\mathbf{r}\right)\) holds for scalar functions. Then,
\[ \begin{eqnarray*}\int_{\Omega}u\left(\mathbf{r}\right)\left(\Delta+k^{2}\right)w\left(\mathbf{r}\right)dV & = & \int_{\Omega}u\left(\mathbf{r}\right)\nabla\cdot\nabla w\left(\mathbf{r}\right)dV+k^{2}\int_{\Omega}u\left(\mathbf{r}\right)w\left(\mathbf{r}\right)dV\\& = & \int_{\Omega}\nabla\left(u\left(\mathbf{r}\right)\nabla w\left(\mathbf{r}\right)\right)-\nabla u\left(\mathbf{r}\right)\cdot\nabla w\left(\mathbf{r}\right)dV+k^{2}\int_{\Omega}u\left(\mathbf{r}\right)w\left(\mathbf{r}\right)dV\\& = & \int_{\partial\Omega}u\left(\mathbf{r}\right)\left(\partial_{\boldsymbol{\mathbf{\nu}}}w\left(\mathbf{r}\right)\right)\cdot d\mathbf{A}-\int_{\Omega}\nabla u\left(\mathbf{r}\right)\cdot\nabla w\left(\mathbf{r}\right)dV+k^{2}\int_{\Omega}u\left(\mathbf{r}\right)w\left(\mathbf{r}\right)dV\end{eqnarray*}\ .\]
Here, we had to apply the divergence theorem \(\int_{\Omega}\nabla\cdot\mathbf{X}\left(\mathbf{r}\right)dV=\int_{\partial\Omega}\mathbf{X}\left(\mathbf{r}\right)\cdot d\mathbf{A}\) (or, in its generalized version \(\int_{\Omega}du=\int_{\partial\Omega}u\), known as Stoke's theorem in two dimensions). Furthermore we have used that we can directly write \(\nabla w\left(\mathbf{r}\right)\cdot d\mathbf{A}=\partial_{\boldsymbol{\nu}}w\left(\mathbf{r}\right)\cdot d\mathbf{A}\) with \(\boldsymbol{\nu}\) being the surface normal of \(\mathbf{A}\) since other parts of the gradient will not contribute.
So we find that the difference becomes
\[\int_{\Omega}u\left(\mathbf{r}\right)\left(\Delta+k^{2}\right)w\left(\mathbf{r}\right)dV-\int_{\Omega}w\left(\mathbf{r}\right)\left(\Delta+k^{2}\right)v\left(\mathbf{r}\right)dV = \int_{\partial\Omega}\left[u\left(\mathbf{r}\right)\partial_{\boldsymbol{\mathbf{\nu}}}w\left(\mathbf{r}\right)-w\partial_{\boldsymbol{\mathbf{\nu}}}u\left(\mathbf{r}\right)\right]d\mathbf{A}\ .\]
The result is independent of \(k\) and the desired Green's second identity.
A Short Reminder: Green's Function
The next step is to replace one of the functions by the Green's function \(G\left(\mathbf{r},\mathbf{r}^{\prime}\right)\). Before we proceed, let us repeat some basics here. The Green's function is sometimes called the the fundamental solution of a differential equation. Given a differential operator \(\mathcal{D}\) like \(\Delta\) (Laplace) or \(\Delta+k^{2}\) (Helmholtz), \(G\left(\mathbf{r},\mathbf{r}^{\prime}\right)\) is defined by
\[\mathcal{D}G\left(\mathbf{r},\mathbf{r}^{\prime}\right)=\delta\left(\mathbf{r}-\mathbf{r}^{\prime}\right)\ ,\]
with \(\mathcal{D}\) acting on \(\mathbf{r}\). Care has to be taken because of the dimensions of a problem. For the Laplace equation, \(\Delta G\left(\mathbf{r},\mathbf{r}^{\prime}\right)=\delta\left(\mathbf{r}-\mathbf{r}^{\prime}\right)\), one finds
\[\text{2D:}\ G\left(\mathbf{r},\mathbf{r}^{\prime}\right)=\frac{1}{2\pi}\log\left(\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\right)\ \text{and in } \text{3D:}\ G\left(\mathbf{r},\mathbf{r}^{\prime}\right)=-\frac{1}{4\pi}\frac{1}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|}\ .\]
We can see that these functions correspond to the potentials of a line and a point charge. For the Helmholtz equation with \(\mathcal{D}=\Delta+k^{2}\), we have (each with two solutions for outgoing and incoming energy)
\[\text{2D:}\ G\left(\mathbf{r},\mathbf{r}^{\prime};k\right)=-\frac{\mathrm{i}}{4}H_{0}^{1/2}\left(k\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\right)\ \text{and } \text{3D:}\ G\left(\mathbf{r},\mathbf{r}^{\prime};k\right)=-\frac{1}{4\pi}\frac{e^{\pm\mathrm{i}k\left|\mathbf{r}-\mathbf{r}^{\prime}\right|}}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|}\ .\]
After this little repitition we may come back to the abstract definition of the Green's function and derive the boundary integral equation.
The Boundary Integral Equation
Ok, let us take the left hand side of Green's second identity and replace \(u\rightarrow\phi\) and \(w\rightarrow G\). We may again use the Helmholtz equation since the results will be the same. Using the definition of the Green's function, we find
\[\int_{\Omega}\phi\left(\mathbf{r}\right)\underbrace{\left(\Delta+k^{2}\right)G\left(\mathbf{r},\mathbf{r}^{\prime};k\right)}_{\delta\left(\mathbf{r}-\mathbf{r}'\right)}d^{2}\mathbf{r}-\int_{\Omega}G\left(\mathbf{r},\mathbf{r}^{\prime};k\right)\underbrace{\left(\Delta+k^{2}\right)\phi\left(\mathbf{r}\right)}_{0}d^{2}\mathbf{r} = \phi\left(\mathbf{r}^{\prime}\right)\ .\]
On the other hand, we know that this equation has to equal the right hand side. So, we conclude that
\[\phi\left(\mathbf{r}^{\prime}\right) = \int_{\partial\Omega}\phi\left(\mathbf{r}\right)\partial_{\boldsymbol{\mathbf{\nu}}}G\left(\mathbf{r},\mathbf{r}^{\prime};k\right)d\mathbf{A}-\int_{\partial\Omega}G\left(\mathbf{r},\mathbf{r}^{\prime};k\right)\partial_{\boldsymbol{\mathbf{\nu}}}\phi\left(\mathbf{r}\right)d\mathbf{A}\ .\]
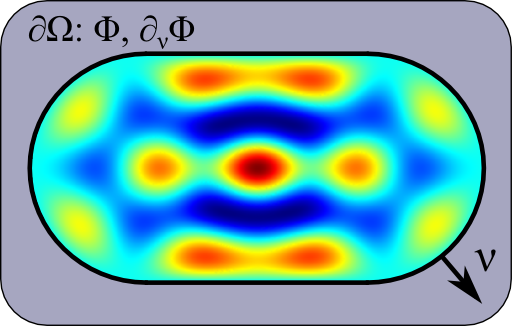 The latter equation is the boundary integral equation. So, knowing the Green's function, we can can determine the potential \(\phi\) inside the domain Ω just from its values and derivatives at the domain's boundary \(\partial\Omega\). On the right, you can see an example of a certain geometry with Dirichlet boundary conditions, calculated for the Helmholtz equation in two dimensions (translation invariance in one direction, regarding it as a certain kind of waveguide) using the Boundary Element Method which will be discussed in the following.
The latter equation is the boundary integral equation. So, knowing the Green's function, we can can determine the potential \(\phi\) inside the domain Ω just from its values and derivatives at the domain's boundary \(\partial\Omega\). On the right, you can see an example of a certain geometry with Dirichlet boundary conditions, calculated for the Helmholtz equation in two dimensions (translation invariance in one direction, regarding it as a certain kind of waveguide) using the Boundary Element Method which will be discussed in the following.
The Boundary Element Method
We can rewrite the boundary integral equation in the form
\[0 = \int_{\partial\Omega}\phi\left(\mathbf{r}\right)\left[\partial_{\boldsymbol{\mathbf{\nu}}}G\left(\mathbf{r},\mathbf{r}^{\prime};k\right)-\delta\left(\mathbf{r}-\mathbf{r}^{\prime}\right)\right]d\mathbf{A}-\int_{\partial\Omega}G\left(\mathbf{r},\mathbf{r}^{\prime};k\right)\partial_{\boldsymbol{\mathbf{\nu}}}\phi\left(\mathbf{r}\right)d\mathbf{A}\]
taking the electrostatic potential again into the integral. This equation can now be re-interpreted as an integral operator acting on the potential and its derivative
\[0 = \mathcal{M}\left(\begin{array}{c}\phi\\\partial_{\boldsymbol{\nu}}\phi\end{array}\right)\ .\]
Then, one can discretize the operator \(\mathcal{M}\rightarrow M\) where \(M\) now is some matrix with discretized values of \(\left[\partial_{\boldsymbol{\mathbf{\nu}}}G\left(\mathbf{r}_{i},\mathbf{r}_{j};k\right)-\delta_{\mathbf{r}_{i},\mathbf{r}_{j}}\right]\Delta\mathbf{A}_{i}\) acting on discretized \(\phi\left(\mathbf{r}_{i}\right)\) in the upper left part and \(-G\left(\mathbf{r}_{i},\mathbf{r}_{j};k\right)\Delta\mathbf{A}_{i}\) acting on \(\partial_{\boldsymbol{\nu}}\phi\left(\mathbf{r}_{i}\right)\) in the lower right part.
We can now evaluate \(M\) for example to find the resonances of some dielectric body since the system of equations only has a solution if the (resonance condition) \(\det M=0\) holds. We may also combine different domains to have different \(\Omega_i\) respecting the appropriate boundary conditions in-between. In all cases we will come to the point where we actually have to compute the elements of \(M\).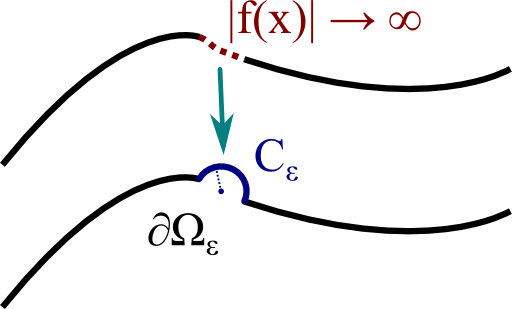 However, evaluating the elements of \(M\) can be quite problematic on the diagonal. here, \(i=j\) and \(\mathbf{r}_{i}=\mathbf{r}_{j}\), so we have to evaluate the Green's function at a vanishing distance where it is singular. In two dimensions using complex integration, one can evaluate the diagonal elements in terms of a Cauchy principal value integral.
However, evaluating the elements of \(M\) can be quite problematic on the diagonal. here, \(i=j\) and \(\mathbf{r}_{i}=\mathbf{r}_{j}\), so we have to evaluate the Green's function at a vanishing distance where it is singular. In two dimensions using complex integration, one can evaluate the diagonal elements in terms of a Cauchy principal value integral.
Here, the integral over a singular point of some function is replaced by an integral leaving out a certain infinitesimal part \(\epsilon\) and taking the limit \(\epsilon\rightarrow0\). One has to further consider the integration over a small \(\epsilon\)-semicircle, see figure on the left. Then, one can even achieve approximate analytical solutions for the diagonal elements as it was done in “Boundary element method for resonances in dielectric microcavities” and discussed in the background below. This is crucial since otherwise such calculations can be computationally extremely demanding.
Background: The Boundary Element Method
 Using Green's second identity, the boundary integral equation relates the values of the electrostatic potential inside some domain Ω to its values at the boundary of Ω. This is per se not really useful because we might be able to study just a single dielectric body in some embedding medium. However, the approach can be generalized to several domains, i.e. more complex bodies - examples for such bodies can be seen on the left: a) a photonic crystal embedded in some metal, b) a (much) more sophisticated structure.
Using Green's second identity, the boundary integral equation relates the values of the electrostatic potential inside some domain Ω to its values at the boundary of Ω. This is per se not really useful because we might be able to study just a single dielectric body in some embedding medium. However, the approach can be generalized to several domains, i.e. more complex bodies - examples for such bodies can be seen on the left: a) a photonic crystal embedded in some metal, b) a (much) more sophisticated structure.
The generalization is done using the appropriate boundary conditions between adjacent domains. This leads to a system of coupled boundary integral equations which can be discretized replacing the integrals by sums. In turn, the system of boundary integral equations can be evaluated on a computer - the numerical approach is called “Boundary Element Method”.
It has a lot of applications in optics, acoustics, aerodynamics since one can use this this method also for other kinds of wave equations. Within the Boundary Element Method, several scientific and engineering questions can be cast into questions on the arising system of equations, hence properties of some matrix. For instance, one can calculate the response of a dielectric body to a giving excitation or a direct computation of the resonances.
A lot of books and papers exist. For a realization with an optics/nanophotonics background, see J. Wierig's excellent “Boundary element method for resonances in dielectric microcavities”, Journal of Optics A: Pure and Applied Optics 5, 2003.
Journal Page | arXiv | PDF